Sword Offer Problems

algorithm

Sword Offer Problems

1. Duplicated Integers in Array

In an array of size n, all entries are integers and are in the range [0, n-1]. However, there are some duplicated integers. Please find out an arbituary duplicated integer. For example:

1
2
3
4
5
6
Input:
n = 7, array:[2, 3, 1, 0, 2, 5, 3]


Output:
2 or 3, since 2 and 3 are duplicated entries.

To solve this problem, we can use hashtable, and the time complexity is O(n). However, the space complexity is also O(n), can we reduce space complexity?

We know that all entries are in the range [0, n-1], suppose there is no duplicate, when we sort the array in ascending order, the integer at index i would be i, namely:

[0, 1, 2, ... , n-2, n-1]

Because there are some duplicates, if we rearrange the array to make sure that the integer at index i is i, there are two possibilities for the rearranged array:

  1. there is no entry at index i

  2. there are two or more entries at index i

Take [2, 3, 1, 0, 2, 5, 3] as an example, we can scan and rearrange the array like this:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
We start from index 0:

[2, 3, 1, 0, 2, 5, 3]
 ⬆

2 should be at index 2, therefore we swap it with the integer at index 2:

[1, 3, 2, 0, 2, 5, 3]
 ⬆

1 should be at index 1, therefore we swap it with the integer at index 1:

[3, 1, 2, 0, 2, 5, 3]
 ⬆

3 should be at index 3, therefore we swap it with the integer at index 3:

[0, 1, 2, 3, 2, 5, 3]
 ⬆

0 is at index 0, we can skip to the next index:

[0, 1, 2, 3, 2, 5, 3]
    ⬆

1 is at index 1, we can skip to the next index:

[0, 1, 2, 3, 2, 5, 3]
       ⬆

2 is at index 2, we can skip to the next index:

[0, 1, 2, 3, 2, 5, 3]
          ⬆

3 is at index 3, we can skip to the next index:

[0, 1, 2, 3, 2, 5, 3]
             ⬆

2 should be at index 2, and when we swap it with the integer at index 2, we find out that 
the integer at index 2 is also 2. Therefore 2 is duplicated and we can return 2.

In this way, the time complexity is O(n), and because we just modify the original array and do not need to allocate extra memory, the space complexity is O(1).

If the problem does not allow us to modify the original array, we need to have an extra array of size n, and then traverse the original array, copy each entry into the new array:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
We start from index 0:

original array: [2, 3, 1, 0, 2, 5, 3]
                 ⬆
new array: [ , , , , , , ]

2 should be at index 2, therefore we copy it and put it into the new array at index 2:

original array: [2, 3, 1, 0, 2, 5, 3]
                    ⬆
new array: [ , , 2, , , , ]

3 should be at index 3, therefore we copy it and put it into the new array at index 3:

original array: [2, 3, 1, 0, 2, 5, 3]
                       ⬆
new array: [ , , 2, 3, , , ]

1 should be at index 1, therefore we copy it and put it into the new array at index 1:

original array: [2, 3, 1, 0, 2, 5, 3]
                          ⬆
new array: [ , 1, 2, 3, , , ]

0 should be at index 0, therefore we copy it and put it into the new array at index 0:

original array: [2, 3, 1, 0, 2, 5, 3]
                             ⬆
new array: [ 0, 1, 2, 3, , , ]

2 should be at index 2, therefore we need to copy it and put it into the new array at index 2. However, position 2 has already been taken. Therefore 2 is duplicated.

In this way, the time and space complexity are all O(n). Can we reduce the space complexity?

There is a trade-off between time complexity and space complexity, if we want to reduce the space complexity, we need to increase time complexity. Take [2, 3, 1, 0, 2, 5, 3] as an example, we can use binary search to solve this problem:

  • The length of [2, 3, 1, 0, 2, 5, 3] is 7, therefore we know that all the entries are in the range [0,6]. We split the array into two parts based on the middle value (0+6)/2 = 3:

    • one part is from 0 to 3, i.e. [2, 3, 1, 0, 2, 3]
    • the other part is from 4 to 6, i.e [5]

  • There are 5 integers from 4 to 6, which means there is no duplicate in this part. There are 6 integers from 0 to 3, if there is no duplicte, there should be 4 integers, therefore we know there are duplicates in this part.

  • For the part [2, 3, 1, 0, 2, 3], we split the array into two parts based on the middle value (0+3)/2 = 1:

    • one part is from 0 to 1, i.e. [1, 0]
    • the other part is from 2 to 3, i.e [2, 3, 2, 3]

  • There are 2 integers from 0 to 1, which means there is no duplicate in this part. There are 4 integers from 2 to 3, if there is no duplicte, there should be 2 integers, therefore we know there are duplicates in this part.

  • For the part [2, 3, 2, 3], we split the array into two parts based on the middle value (2+3)/2 = 2:

    • one part is from 2 to 2, i.e. [2, 2]
    • the other part is from 3 to 3, i.e [3, 3]

  • There are 2 integers from 2 to 2, which means 2 is duplicated. There are 2 integers from 3 to 3, which means 3 is also duplicated.

Here is the code:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
public class DuplicatedArray {
    public static int getDuplicate(int[] arr) {
        if (arr.length == 0) {
            return -1;
        }

        int left = 0;
        int right = arr.length - 1;

        while (left <= right) {
            int mid = left + ((right - left) >> 1);// left + (right - left)/2
            int count = countRange(arr, left, mid);

            if (left == right) {
                if (count > 1) {
                    return left;
                } else {
                    break;
                }
            }

            if (count > mid - left + 1) {// there are duplicates in the range [left, mid]
                right = mid;// keep binary searching in the range [left, mid]
            } else {// there is no duplicate in the range [left, mid]
                left = mid + 1;// searching in the range [mid + 1, right]
            }

        }
        return -1;
    }


    /**
     * given an array of integers, countRange counts the number
     * of integers in the range [left, right]
     * for example:
     * <p>
     * arr = [0, 1, 2, 3, 4, 5], left = 1, right = 3
     * the number of integers in range [1,3] is 3
     */
    public static int countRange(int[] arr, int left, int right) {
        int count = 0;

        for (int i = 0; i < arr.length; i++) {
            if (arr[i] >= left && arr[i] <= right) {
                count++;
            }
        }

        return count;
    }

    public static void main(String[] args) {
        int[] arr = new int[]{2, 3, 1, 0, 2, 5, 3};
        System.out.println(getDuplicate(arr));// 2

        arr = new int[]{6, 3, 1, 0, 2, 5, 3};
        System.out.println(getDuplicate(arr));// 3
    }

}

For the above code, the time complexity is O(nlogn) and the space complexity is O(1). We reduce the space complexity by increasing the time complexity.

2. Replace Space with “%20”

Given a String, replace all the spaces in the String with “%20”. For example:

1
2
3
4
5
Input: 
"We are happy."

Output:
"We%20are%20happy."

To solve this problem, we can use StringBuilder:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
public class ReplaceWithSpace {
    public static String replace(String str) {
        StringBuilder sb = new StringBuilder();
        char[] chars = str.toCharArray();
        for (int i = 0; i < chars.length; i++) {
            if (chars[i] == ' ') {
                sb.append("%20");
            } else {
                sb.append(chars[i]);
            }
        }
        return sb.toString();
    }

    public static void main(String[] args) {
        System.out.println(replace("We are happy."));
    }
}

3. Print a Singly-linked List in Reverse Order

Given a head pointer of a singly-linked list, print the value of each node in reverse order.

There are two ways to solve this problem:

  1. Iteration: We can traverse the linked list, and put each node’s value into a stack. Then we can pop and print the values from the stack.

  2. Recursion: Actually, recursion also makes use of a stack, i.e. the call stack.

Here is the code for recursion:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
public class PrintLinkedListInReverseOrder {
    public static void print(ListNode head) {
        ListNode current = head.next;
        if(current == null) {
            return;
        }
        print(current);
        System.out.println(current.val);
    }

    public static void main(String[] args) {
        ListNode head = new ListNode();
        ListNode node1 = new ListNode(1);
        ListNode node2 = new ListNode(2);
        ListNode node3 = new ListNode(3);
        ListNode node4 = new ListNode(4);

        head.next = node1;
        node1.next = node2;
        node2.next = node3;
        node3.next = node4;

        print(head);
    }
}

class ListNode {
    int val;
    ListNode next;

    ListNode() { }

    ListNode(int val) {
        this.val = val;
    }
}

4. Rebuild a Binary Tree

Rebuild a binary tree based on the preorder traversal and inorder traversal result. For example, given the preorder traversal {1, 2, 4, 7, 3, 5, 6, 8} and the inorder traversal {4, 7, 2, 1, 5, 3, 8, 6}, we can rebuild the following binary tree:

1
2
3
4
5
6
7
      1
    /   \
   2     3
 /      /  \
4      5    6
  \        /
   7      8

We know that for preorder traversal, the first node to be traversed is always the root node, then we traverse the left subtree, and then the right subtree. And for inorder traversal, we traverse left subtree first, then the root node and the right subtree. Therefore, by combining the two traversals, we can find out the root node, left subtree and right subtree:

sword_offer_problems_1

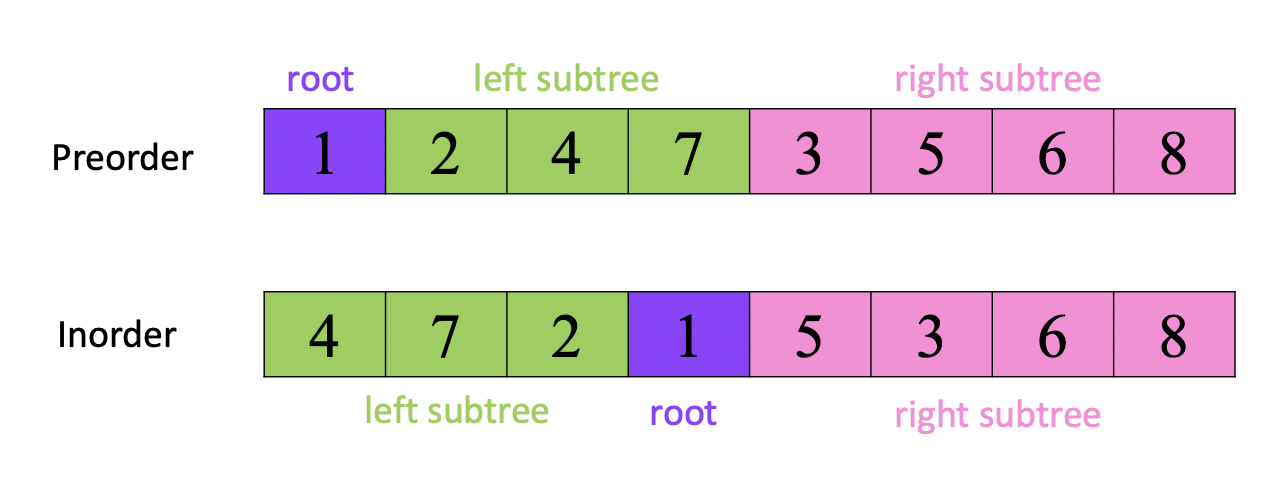
For the left subtree and right subtree, we can find out the root node, leftsubtree and right subtree recursively.

Here is the code to solve the problem:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
public class ReconstructBinaryTree {

    public static TreeNode reconstruct(int[] preOrder, int[] inOrder) {
        TreeNode root = reconstruct(preOrder, 0, preOrder.length - 1,
                inOrder, 0, inOrder.length - 1);
        return root;
    }

    private static TreeNode reconstruct(int[] preOrder, int startPre, int endPre,
                                        int[] inOrder, int startIn, int endIn) {

        if (startPre > endPre || startIn > endIn) {
            return null;
        }
        TreeNode root = new TreeNode(preOrder[startPre]);

        for (int i = startIn; i <= endIn; i++)
            if (inOrder[i] == preOrder[startPre]) {
                root.left = reconstruct(preOrder, startPre + 1, startPre + i - startIn, inOrder, startIn, i - 1);
                root.right = reconstruct(preOrder, startPre + i - startIn  + 1, endPre, inOrder, i + 1, endIn);
                break;
            }

        return root;
    }

}

class TreeNode {
    int val;
    TreeNode left;
    TreeNode right;

    TreeNode() {
    }

    TreeNode(int val) {
        this.val = val;
    }

    TreeNode(int val, TreeNode left, TreeNode right) {
        this.val = val;
        this.left = left;
        this.right = right;
    }
}

5. The Next Node of Binary Tree

Given a binary tree and a node, how can we find the next node of this node according to the inorder traversal? For example, we have a tree like this:

sword_offer_problems_2

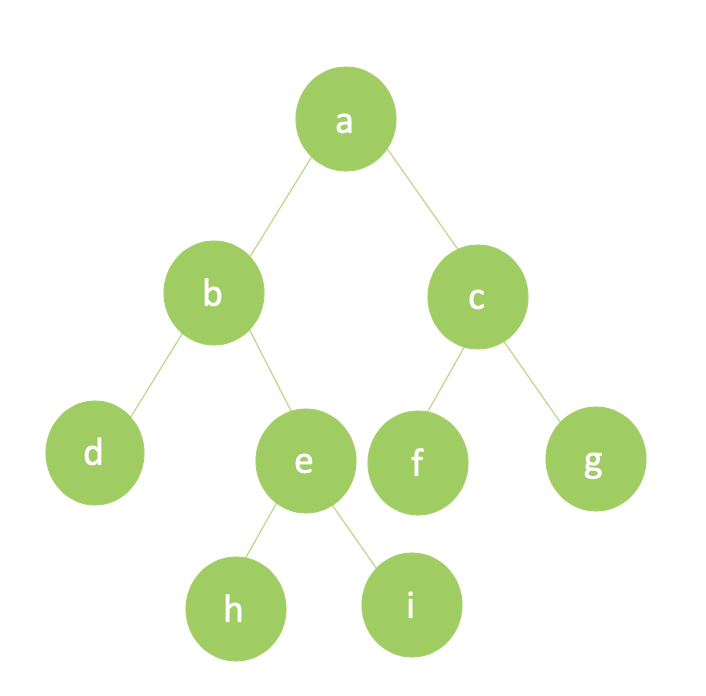
And we know that the inorder traversal of the tree is {d, b, h, e, i, a, f, c, g}.

According to the inorder traversal, d‘s next node is b, b‘s next node is h…

How can we implement this in Java? There are two cases:

  1. If a node has right subtree: for example, the node a, its next node is the leftmost node of its right subtree, i.e. f.

  2. If a node does not have right subtree:

    1. If this node is the left child of its parent node, say h, then the parent node e is the next node.
    2. If this node is the right child of its parent node, say i, to find its next node, we need to find its parent node e. Because e is its parent node b‘s right child, we keep going up to b, and because b is its parent node a‘s left child, we can know b‘s parent node a is i‘s next node. To sum up, we should firstly find a node, which is the parent node of i, or the parent’s parent…, and this node should also be the lelf child of its own parent node. If we can find a node like this, then this node’s parent node is the next node of i. If we cannot find a node like this(e.g. the node g), then we can say g is the last node, which does not have a next node.

Here is the Java code:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
public class GetNextNode {
    public TreeNode getNext(TreeNode node) {

        if (node == null) {
            return null;
        }

        // the node has right subtree, its next node is
        // the leftmost node of its right subtree
        if (node.right != null) {
            node = node.right;

            while (node.left != null) {
                node = node.left;
            }

            return node;
        }

        //  the node does not have right subtree, and it
        //  is not the root node
        while (node.parent != null) {

            if (node.parent.left == node) {
                return node.parent;
            }

            node = node.parent;
        }

        return null;//we keep going up to the root node, and still cannot find the next node
    }

}

class TreeNode {
    char value;
    TreeNode left;
    TreeNode right;
    TreeNode parent;
}

6. Using Two Stacks to Implement a Queue

We know that a stack is LIFO(last in, first out), and a queue is FIFO(first in, first out). For stack, we have the method push and pop, and for queue, we have the method enqueue and dequeue. Considering the properties of stack and queue, we can use two stacks to implement a queue:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
import java.util.Stack;

public class StackImplQueue<E> {
    Stack<E> stack1 = new Stack<>();// stack1 is used to enqueue
    Stack<E> stack2 = new Stack<>();// stack2 is used to reverse order

    public boolean isEmpty() {
        return stack1.isEmpty() && stack2.isEmpty();
    }

    public int size() {
        return stack1.size() + stack2.size();
    }

    public void enqueue(E e) {
        stack1.push(e);
    }

    public E dequeue() {
        // if stack2 is not empty, pop the top of stack2 directly,
        // else push all the elements from stack1 to stack2
        if (stack2.isEmpty()) {
            while (!stack1.isEmpty()) {
                stack2.push(stack1.pop());
            }
        }
        return stack2.pop();
    }
}

Here is a good video to explain the above code: https://www.youtube.com/watch?v=AN0axYeLue0

Similarly, we can use two queues to implement a stack, and here is a good video about how to do this: https://www.youtube.com/watch?v=ww5Ac232WEU

7. Sorting Ages

Suppose we have a big array, which stores the ages of many people. Now we want to sort the ages, and the time complexity should be O(n). We can reduce the time complexity by increasing the space complexity, i.e. using an extra array timesOfAge:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
public class SortAges {
    public static void sortAges(int[] ages) {
        if (ages.length <= 0) {
            throw new IllegalArgumentException("Invalid Parameters");
        }

        int length = ages.length;

        // we assume that the range of ages is [0-99]
        // timesOfAge[18] = 25 means that there are 25 people whose age is 18.
        int[] timesOfAge = new int[99 + 1];

        // scan the ages array, and record how many times each age occurs in the array
        // the time complexity of this part is O(n)
        for (int i = 0; i < length; i++) {
            if (ages[i] < 0 || ages[i] > 99) {
                throw new IllegalArgumentException("Invalid Parameter");
            }

            int age = ages[i];
            ++timesOfAge[age];
        }

        // starting from age 0, if timesOfAge[0] = 3, 
        // we set ages[0], ages[1] and ages[2] to 0; if timesOfAge[1] = 2,
        // we set ages[3] and ages[4] to 1, so on and so forth...
        // after traversing the timesOfAge array, the ages array is
        // sorted in ascending order, e.g. [0, 0, 0, 1, 1, 2 ....]
        // the time complexity of this part is 100*O(n)
        int index = 0;
        for (int i = 0; i < timesOfAge.length; i++) {
            for (int j = 0; j < timesOfAge[i]; j++) {
                ages[index] = i;
                index++;
            }
        }
    }
}

As shown, the time complexity of the above code is O(n) + 100*O(n) = O(n).

8. Cut the Rope

Given a rope of length n, we can cut it into m parts(m, n are integers and m>1, n>1). Each part i of the rope is recorded as k[i], i.e. k[1], … , k[m]. Now we want to know the maximum value of k[1]x…xk[m].

For example, if n=8, when we cut the rope into 3 parts(m=3), i.e. k[1]=2,k[2]=3,k[3]=3. In this way, we can get the maximum product of k[i], which is 18.

The first way to solve this problem is to use dynamic programming:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
package sword_offer;

public class CutRope {

    // using dynamic programming
    public static int cutRopeDP(int n) {

        // why we need this "return" part? See below comments.
        if (n < 2) return 0;
        if (n == 2) return 1;
        if (n == 3) return 2;

        int[] dp = new int[n + 1];
        // dp[0] = 0;

        // when the rope is of length 1, 2 or 3, we do not cut it into pieces,
        // i.e. dp[1],dp[2] and dp[3] do not store the correct answer,
        // that is why we need the above "return" part
        dp[1] = 1;
        dp[2] = 2;
        dp[3] = 3;
        
        for (int i = 4; i <= n; i++) {
            for (int j = 1; j <= i / 2; j++) {
                dp[i] = Math.max(dp[i], dp[i - j] * dp[j]);
            }
        }

        return dp[n];
    }
}

As shown above, we start with the simplest case, i.e. the rope is of length 0 or 1, we cannot cut the rope, therefore we return 0.

When the rope is of length 2, we can only cut it into two parts, i.e. k[1] = k[2] = 1, and the product is 1. Therefore we return 1.

When the rope is of length 3, we can cut it into 3 parts(k[1]=k[2]=k[3]=1) or 2 parts(k[1]=1, k[2]=2), and the maximum product is 2.

Then, when the rope is of length 4, we can cut it once, into 1+3 or 2+2, and we can know that dp[4] = max(dp[1]*dp[2], dp[2]*dp[2]).

By using dynamic programming, the time complexity is O(n^2) and the space complexity is O(n)(we use a dp array to store the results).

9. Number of 1s

Given an integer, output the number of 1s in the binary representation of this integer. For example, given the integer 9, which is 1001 in binary, the number of 1s is 2, therefore we output 2.

We can use bit manipulation to solve this problem.Take integer 9 as an example:

  • (1001 & 0001) != 0, and we can know the fourth digit of 9 is 1

  • (1001 & 0010) == 0, and we can know the third digit of 9 is not 1

  • (1001 & 0100) == 0, and we can know the second digit of 9 is not 1

  • (1001 & 1000) != 0, and we can know the second digit of 9 is 1

Therefore there are two 1s in 9. Here is the code:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
public class NumOfOnes {
    public static int numOfOnes(int n) {
        int result = 0;
        int temp = 1;
        while (temp != 0) {// 0000 0001 -> 0000 0010 -> ... -> 1000 0000 -> 0000 0000
            result = (n & temp) != 0 ? result + 1 : result;
            temp = temp << 1;
        }

        return result;
    }

    public static void main(String[] args) {
        System.out.println(numOfOnes(9));
    }
}

And here is a good video to explain this problem: https://www.bilibili.com/video/BV1Y7411z7Yv?from=search&seid=1959341215906372645

10. Print From 1 to Maximum n-digit Number

Given an integer n, print from 1 to the maximum n-digit number. For example, given the integer 3, the maximum n-digit number is 999, therefore we should print 1,2,3… to 999.

As n can be very large, the maximum n-digit number could be larger than the maximum long integer. Therefore we can use n-digit String to represent each number.

For example, if n = 3, we can use “001” to represent 1, “002” to represent 2, … “999” to represent 999. And when we print each String, we should erase the 0s in the prefix.

Now, our problem becomes: given a String of length n, each digit of the String can be filled with “0”, “1”, “2”, …, “9”, how many possible combinations are there?

To solve this problem, we should use DFS:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
public class Print1ToMaxOfNDigits {
    public static void Print1ToMaxOfNDigits(int n) {
        if (n < 0) {
            return;
        }

        StringBuffer digits = new StringBuffer(n);
        // initialize digits as "0000...00"
        for (int i = 0; i < n; i++) {
            digits.append('0');
        }


        for (int i = 0; i < 10; i++) {
            // set the first digit of the string, i.e. "0000...00", "1000...00", ..., "9000...00"
            digits.setCharAt(0, (char) (i + '0'));
            // set the following digits recursively
            dfs(digits, n, 0);
        }

    }

    public static void dfs(StringBuffer digits, int n, int index) {
        if (index == n - 1) {// index starts from 0 to n-1
            printNumber(digits);
            return;
        }

        for (int i = 0; i < 10; i++) {
            digits.setCharAt(index + 1, (char) (i + '0'));
            dfs(digits, n, index + 1);
        }
    }


    public static void printNumber(StringBuffer digits) {
        boolean isBeginning0 = true;

        // actually we can use two for-loops:
        // the first one is to find the first non-zero digit,
        // and the second one is to print the digits starting 
        // from the first non-zero digit
        for (int i = 0; i < digits.length(); i++) {

            // the "first" for-loop 
            if (isBeginning0 && digits.charAt(i) != '0') {
                isBeginning0 = false;
            }

            // the "second" for-loop
            if (!isBeginning0) {
                System.out.print(digits.charAt(i));
            }
        }
        System.out.println();
    }
}

As shown, for DFS, each layer has each its own responsibility, that is, it just need to set the corresponding digit(from 0 to 9), and then deliver the job to the deeper layers. The process is like this: