Statistics&Probability: Confounding

statistics&probability

Statistics&Probability: Confounding

Confounding

When we study association, we should understand that:

association ≠ causation

Association never equals causation, no matter how strong the association it is.

Association is symmetric between two variables X and Y. For example, if you find a strong association between watching television and live longer, it could be the other way around. That if you live longer, you tend to watch more television. However, causation is symmetric.

Suppose we know that there is a strong association between variable X and Y, i.e., X~Y. Let’s consider different scenarios of this association:

  1. scenario 1: X causes variation in Y(X has a causal effect on Y, X and Y have a cause-effect relation), i.e., X->Y. For example, smoking causes cancer.

  2. scenario 2: We have a third variable Z that causes variation in both X and Y. For example, Z can be the size of a fire, and Y is the damages caused by the fire, and the X is number all firefighters at the scene of the fire.

1
2
3
X ~ Y
 ↖️ ↗️
  Z
  1. scenario 3: We have X and Y. We observe association between X and Y:

confounding_1

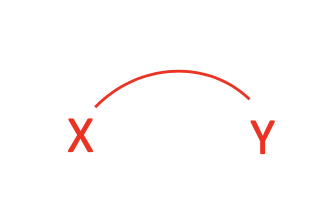
And we sort of suspected that there might be a causation here. Therefore, there is a question mark whether you want to establish causation here:

confounding_2

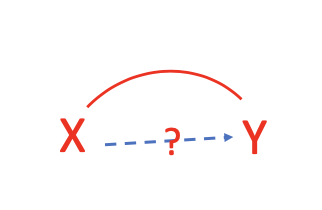
There is a third variable Z that also potentially causes variation in Y:

confounding_3

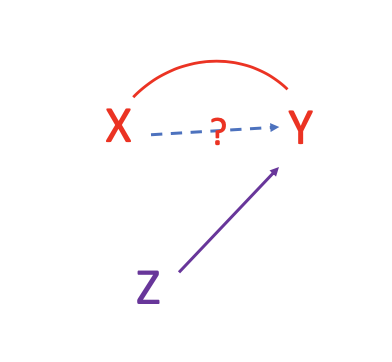
At the same time X and Z are associated – they are mixed together:

confounding_4

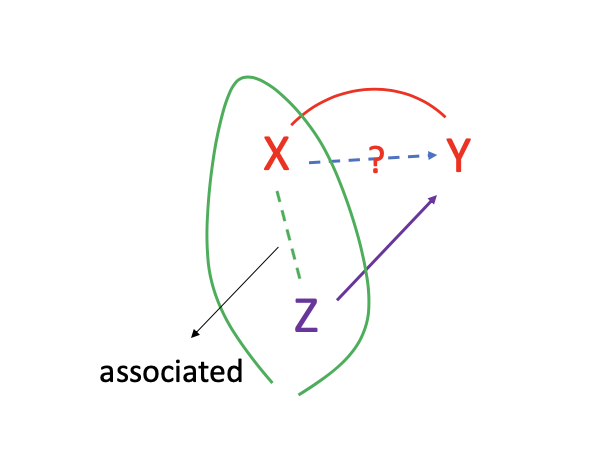
This is called a confounding scenario, where X and Z are associated with each other and they both pretend to have an effect on Y, because they are associated it would be very hard for us to separate the effects.

To make things worse, when Z becomes a hidden confounder, the effect of Z cannot be established using observed data:

confounding_5

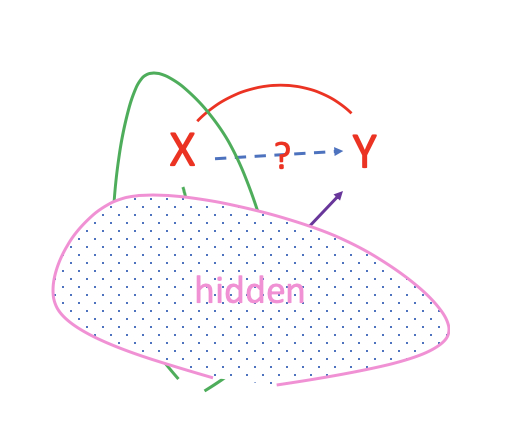
In this case, we can only observe the association between X and Y, but in fact, some of the association can come from Z, because Z and X associated.

One of the phenomena observed when confounding occurs is called the Simpson's paradox.

Establish Cause-effect Relation

How to establish cause-effect relation between two variables? For example, how do we know smoking causes cancer? The most ideal way is to use randomized experiment, such as A/B testing and double blinded experiment.

A/B testing

In A/B testing, we have an experiment with one treatment group A and one control group, B.
And we randomly assign individuals to two groups, and to see whether they exhibit different values in the outcome of interest. The control group is used to:

  1. Create comparison
  2. Control placebo effect

In medical studies, if we gave the treatment group the new medication and give nothing to the people in the control group, the placebo effect may become the hidden confounder. Because the treatment group and the control group differ in two ways.

  1. They differ in the medication received. The group received some new medication. The control received nothing, no medication.

  2. They also differ in the mechanism of the study. One were given a pill or a treatment, and the other received nothing of the similar nature.

Therefore, there are two variables here. And we need create placebo for the control group, such as a sugar pill.

double blinded experiment

In double blinded experiment, each individual do not know which group(treatment group or control group) he/she is assigned. And the people who evaluate the result of the experiment is also blinded, they do not know which group they are evaluated.

The reason for that is knowledge about the group assignments may effect individual reaction to the treatment, and it would also impact the researchers when they evaluate the results from the experiment. Whenever possible we want to keep the experiment double blinded, so to remove potential hidden confounder effects.