Patchwork Knowledge of Statistics and Probability

Individual and Variable

Individual is a unit of observation. And on this unit observation, we observe a set of variables. For example:

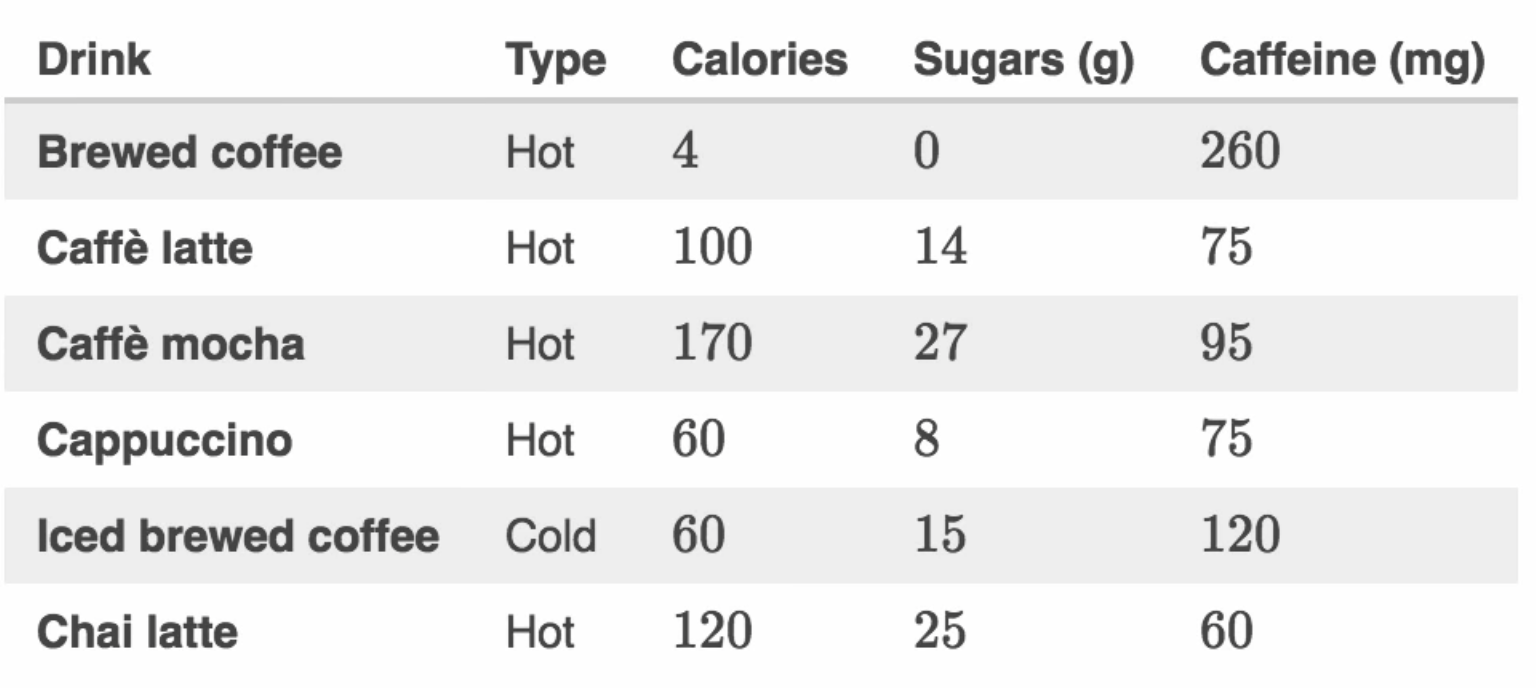
There are three types of variables:

1. Categorical: gender, blood type, etc.
2. Quantitative/numerical: age, height, etc.
3. Ordinal: the values represent ordered categories, for example, “How often do you exercise?” – Everyday, frenquently, sometimes, rarely, never.

Besides, we should know the mathematical notations in statistics. For a data set, we use n for sample size, or the number of individuals in the data. The variables are represented by letters that are close to the end of the alphabet, such as X, Y and Z. We use letter i to index the individuals. Therefore Xi would refer to the value of variable X for the ith individual. One important notation in statistics is the summation sign ∑ . For example:

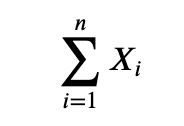
The above equation would mean a sum of the n values from X1 to Xn.

---

Median

Midian is mid-point. Suppose we have the following array:

[100, 100, 85, 90, 75]

What is the median number? Firstly we should sort the numbers:

[75, 85, 90, 100, 100]

Then we can find the median number at the middle of the array, which is 90.

In another case, if we have the following sorted array:

[75, 85, 90, 95, 100, 100]

The median number of the above array is (90 + 95) / 2 = 92.5.

One thing worth noting is that, mean and median are both use to summarize center of variation, but what is the difference between them?

When the data comes with a few extremely large values, the mean is more affected by them than the median, because the mean is numerical average of the entire set of observed values.One large value can drag the average towards it, and that makes the center moves with this extreme value. As for the median, it is not so sensitive.

It is always helpful to look at both mean and median, which give you more complete picture of where the center of variation is.

---

Midrange

Suppose we have the following array:

[100, 100, 85, 90, 75]

What is the midrange? Firstly we should sort the numbers:

[75, 85, 90, 100, 100]

And the midrange is computed like this:

midrange = (highest number + lowest number) / 2 = (75 + 100) / 2 = 87.5

---

Mode

The mode is the most common data. Suppose we have the following array:

[100, 100, 85, 90, 75]

The mode is 100, which show up 2 times.

---

Percentile and Quantile

Percentile is a threshold of a variable that is defined to have a percent of data below it.

For example, for SAT exam, a score 600 is the 79th percentage. This means, if a student receives 600 in SAT exam, then we can know on average there are 79% of all the people who have taken this exam scored below this individual.

Quantiles are a set of special percentiles, which correspond to 25%, 50%(i.e., median) and 75% and divide data into quarters.

To visualize quantiles, we can use box plot. Here is how to draw the box plot:

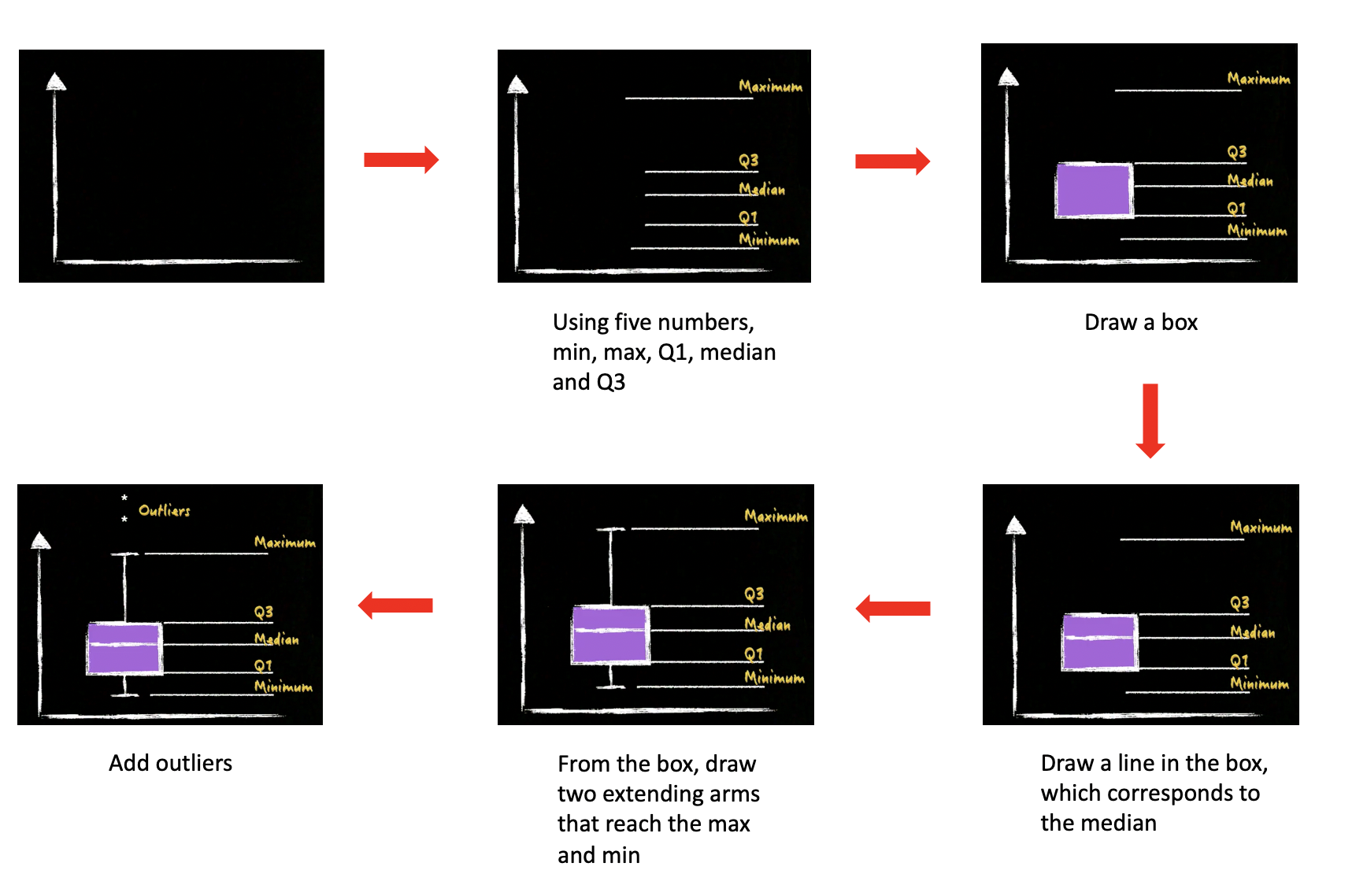
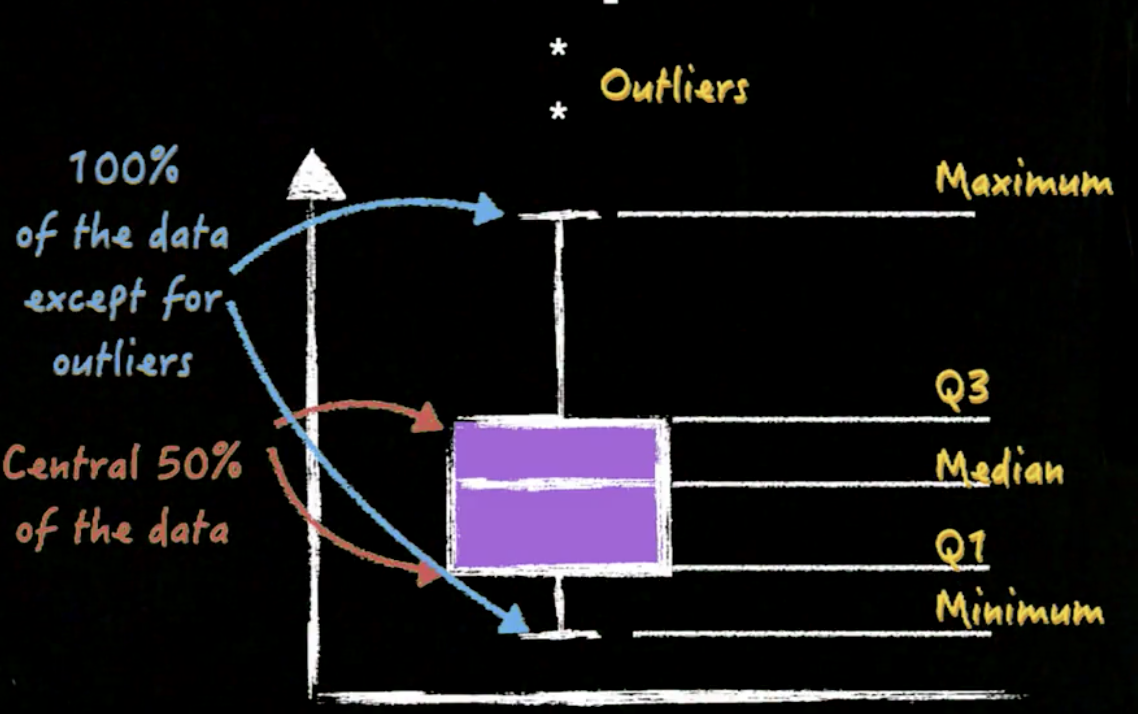
Note that, in the above plot, the maximum/minimum are not the exact minimum/maximum of the observed data. There is a related method to identify possible outliers. If the method regards certain observation as outliers or extreme values, they will not be included in the calculation of the minimum and maximum for the purpose of the box plot. Instead, these values will be added
as outliers.

---

Observational Data

Observational data are data that are gathered by observing real world activity and by contrast with data that come from designed experiments.

---