LeetCode Problem: Top Interview Questions

1. Reverse String

Write a function that reverses a string. The input string is given as an array of characters char[]. Do not allocate extra space for another array, you must do this by modifying the input array in-place with O(1) extra memory. You may assume all the characters consist of printable ascii characters. For example:

Example 1:
Input: ["h","e","l","l","o"]
Output: ["o","l","l","e","h"]

Example 2:
Input: ["H","a","n","n","a","h"]
Output: ["h","a","n","n","a","H"]

To solve the problem, we need to use two pointers, the process is like this:

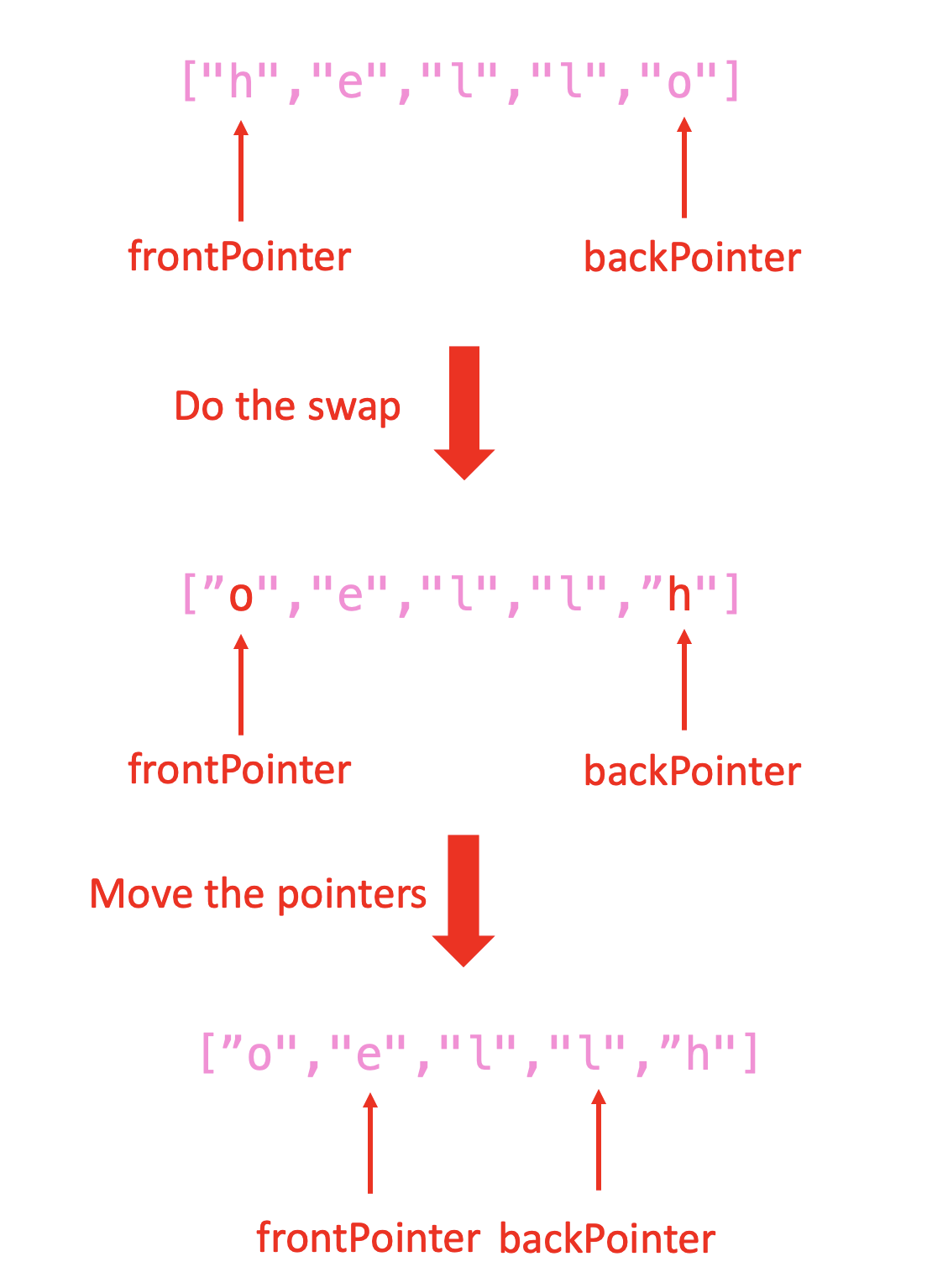
Here is the code of reverse string:

public class ReverseString {
    public void reverseString(char[] s) {
        int frontPointer = 0;
        int backPointer = s.length - 1;// Remember to minus 1!

        while (frontPointer < backPointer) {// There is no need to use "frontPointer <= backPointer"!
            char temp = s[frontPointer];
            s[frontPointer] = s[backPointer];
            s[backPointer] = temp;

            frontPointer++;
            backPointer--;
        }
    }
}

---

2. Single Number

Given a non-empty array of integers, every element appears twice except for one. Find that single one. For example:

Example 1:
Input: [2,2,1]
Output: 1

Example 2:
Input: [4,1,2,1,2]
Output: 4

Note:

Your algorithm should have a linear runtime complexity. Could you implement it without using extra memory?

Using HashSet

The first way is to use HashSet, which uses hash table to implement set. The reason why we use HashSet is that, for the HashSet, the add and remove operations are all in O(1). When we use for loop, the time complexity is O(n) in total. However, using HashSet takes extra memory. Take [2, 2, 1, 3, 3] as an example, the process is like this:

1. We add the 1st element 2 into the set.
2. The 2nd element is 2, as 2 is already in the set, we remove 2 from the set.
3. We add the 3rd element 1 into the set.
4. We add the 4th element 3 into the set.
5. The 5th element is 3, as 3 is already in the set, we remove 3 from the set.
6. After traversing [2, 2, 1, 3, 3], there is only 1 in the set, which is the single number.

The code is like this:

import java.util.HashSet;
import java.util.Set;

public class SingleNumber {
    public int singleNumber(int[] nums) {
        Set<Integer> set = new HashSet<>();

        for (int i : nums) {
            if(set.contains(i)) {
                set.remove(i);
            }else {
                set.add(i);
            }
        }

        for (int i: set) {
            return i;
        }

        return -1;
    }
}

Using Bit Manipulation

A more clever way is to use Bitwise XOR, we know that:

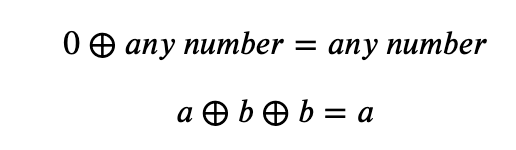
Take [2, 2, 1, 3, 3] as an example:

1 XOR 2 XOR 2 = 1, 1 XOR 3 XOR 3 = 1, and then 1 XOR 0 = 1, therefore our final result is 1, which is the single number. Here is the code:

public class SingleNumber {
    public int singleNumber(int[] nums) {
        int result = 0;
        for(int i: nums) {
            result ^= i;
        }
        return result;
    }
}

By the way, we can also use Bitwise AND(&) to check whether a number is odd or even:

if (a & 1 == 1) {
    System.out.println(a+" is odd.");
} else { // a & 1 == 0
    System.out.println(a+" is even.");
}

---

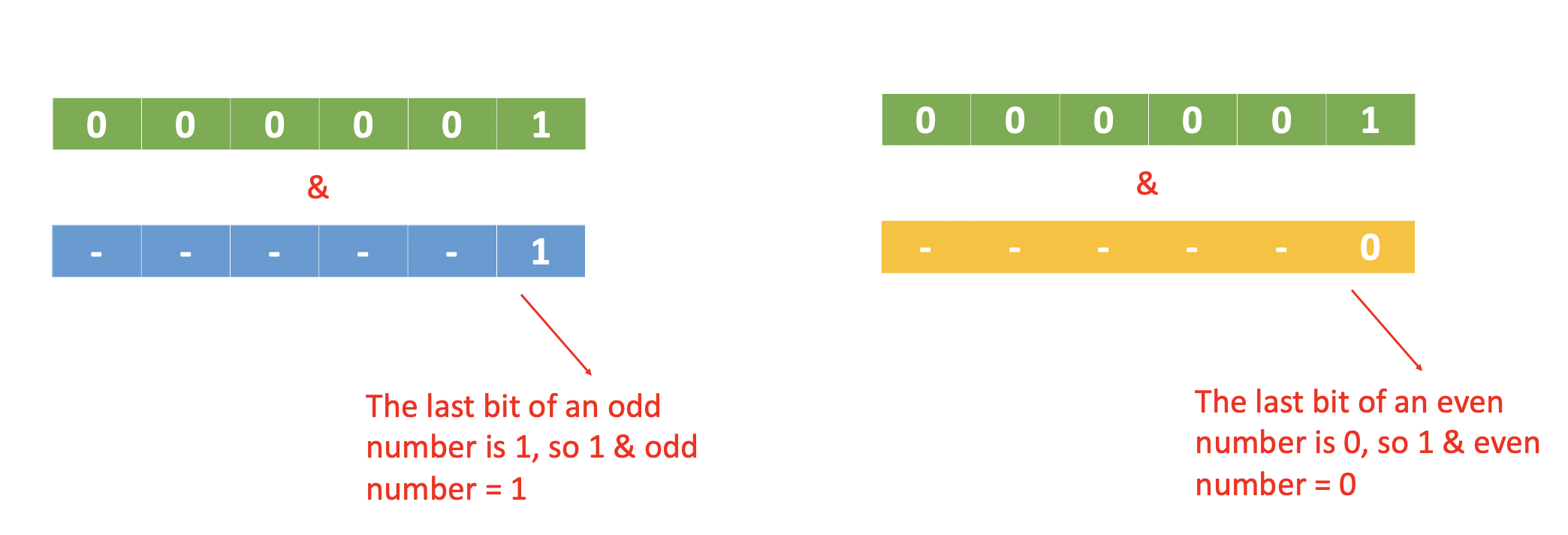
3. Move Zeros

Given an array nums, write a function to move all 0’s to the end of it while maintaining the relative order of the non-zero elements.

Example:

Input: [0,1,0,3,12]
Output: [1,3,12,0,0]

Note:

You must do this in-place without making a copy of the array.
Minimize the total number of operations.

This problem is easy to solve:

public class MoveZeros {
    public void moveZeroes(int[] nums) {
        int index = 0;
        for (int i = 0; i < nums.length; i++) {// firstly place all non-zero values
            if (nums[i] != 0) {
                nums[index] = nums[i];
                index++;
            }
        }

        for (int i = index; i < nums.length; i++) {// then place 0s at the tail of the array
            nums[index] = 0;
            index++;
        }
    }
}

---

4. Power of Two

Given an integer, write a function to determine if it is a power of two. Here is the code:

 public boolean isPowerOfTwo(int n) {
    long i = 1;
    while(i < n) {
        i *= 2;
    }
        
    return i == n;
}

---

5. Majority Element

The easiest way to solve the problem is like this:

 public int majorityElement(int[] nums) {
    if(nums.length == 0) {
        return -1;
    }
        
    // As the majority element appears more than n/2 times,
    // if we sort the array, the element at index n/2 must 
    // be the majority element.
    Arrays.sort(nums);
    return nums[nums.length /2];
}

The common way of solving this problem is using HashMap:

import java.util.HashMap;
import java.util.Map;

public class MajorityElement {
    public int majorityElement(int[] nums) {
        if (nums.length == 0) {
            return -1;
        }

        // <element, frequency>
        Map<Integer, Integer> map = new HashMap<>();
        for (int i : nums) {
            if (!map.containsKey(i)) {
                map.put(i, 1);
            } else {
                map.put(i, map.get(i) + 1);
            }

            if(map.get(i) > nums.length /2) {
                return i;
            }
        }

        return -1;
    }
}

---

6. Roman to Integer

To solve this problem, we need to traverse the input string backward. And there are two cases, addition or subtraction.

For example, if our input string is VI, and at the beginning our result is 0. We traverse I first, and do the addition, our result becomes 0 + 1 = 1. Then we traverse V, as V is larger than I, we do the addition again, and our result becomes 1 + 5 = 6.

If our input string is IV, at the beginning our result is 0. We traverse V first, and do the addition, our result becomes 0 + 5 = 5. Then we traverse I, as I is less than V, we do the subtraction, and our result becomes 5 - 1 = 4.

Here is the code to solve the problem:

import java.util.HashMap;
import java.util.Map;

/**
 * Symbol       Value
 * I             1
 * V             5
 * X             10
 * L             50
 * C             100
 * D             500
 * M             1000
 */
public class RomanToInteger {
    public int romanToInt(String s) {
        Map<Character, Integer> map = new HashMap<>();
        map.put('I', 1);
        map.put('V', 5);
        map.put('X', 10);
        map.put('L', 50);
        map.put('C', 100);
        map.put('D', 500);
        map.put('M', 1000);

        int result = map.get(s.charAt(s.length() - 1));
        for (int i = s.length() - 2; i >= 0; i--) {
            if(map.get(s.charAt(i + 1)) <= map.get(s.charAt(i))) {// "VI", "II"
                result += map.get(s.charAt(i));
            } else {// "IV"
                result -= map.get(s.charAt(i));
            }
        }

        return result;

    }
}

7. Count Primes

Count the number of prime numbers less than a non-negative number, n.

Example:

Input: 10
Output: 4
Explanation: There are 4 prime numbers less than 10, they are 2, 3, 5, 7.

For this problem, if we use brute force, it would be in O(n^2). And the following code is a little efficient, which is in O(n^1.5):

public class CountPrimes {
    public int countPrimes(int n) {
        int count = 0;
        for(int i = 2; i < n;i++) {
            if(isPrime(i)) {
                count++;
            }
        }
       
        return count;
    }
    
    public boolean isPrime(int n) {
         for(int i = 2; i <= Math.sqrt(n); i++) {
            if(n % i == 0) {
                return false;
            }
        }
        
        return true;
    }
}

However, the above code is still too slow. A more efficient way is to use an algorithm called Sieve of Eratoshenes, which is in O(nloglogn).

As shown, the idea of Sieve of Eratoshenes is like this:

1. For the first prime 2, we rule out all its multiples, e.g., 2+2=4, so we rule out 4; 4+2=6, so we rule out 6; 6+2=8, so we rule out 8…

2. For the second prime 3, we rule out all its multiples, e.g., 3+3=6, so we rule out 6; 6+3=9, so we rule out 9; 9+3=12, so we rule out 12…

3. For the third prime 5, we rule out all its multiples, e.g., 5+5=10, so we rule out 10; 10+5=15, so we rule out 15; 15+5=20, so we rule out 20…

4. For the third prime 7, we rule out all its multiples, e.g., 7+7=14, so we rule out 14; 14+7=21, so we rule out 21; 21+7=28, so we rule out 28…

5. Then, all the left numbers, including 2, 3, 5, 7, are prime numbers.

Given a number N, if we want to find all the primes in range[2,N], all we need to do is:

1. Find out all the primes in range[2,sqrt(N)].
2. For each prime in range[2,sqrt(N)], rule out its multiples.

Here is the code to implement this algorithm:

public class CountPrimes {
public int countPrimes(int n) {
        // true: the number is *not* prime.
        // false: the number is prime.
        boolean[] isNotPrime = new boolean[n];

        for(int i = 2; i*i < isNotPrime.length; i++) {
            if(!isNotPrime[i]) {
                for(int j = i + i; j < isNotPrime.length; j+=i) {
                    isNotPrime[j] = true;
                }
            }
        }

        int count = 0;
        for(int i = 2; i< isNotPrime.length; i++) {
            if(!isNotPrime[i]) {
                count++;
            }
        }

        return count;
    }
}

---

8. Sqrt(x)

Implement int sqrt(int x). Compute and return the square root of x, where x is guaranteed to be a non-negative integer. Since the return type is an integer, the decimal digits are truncated and only the integer part of the result is returned.

Example 1:
Input: 4
Output: 2

Example 2:
Input: 8
Output: 2
Explanation: The square root of 8 is 2.82842..., and since the decimal part is truncated, 2 is returned.

Note that we only consider the square root of integers（i.e., 1, 2, 3, …). The first method is brute force:

public int mySqrt(int x) {
    if(x == 0 || x == 1) {
        return x;
    }
    
    // Why should we use long here? Suppose our input x is very large, say x = 2147395600,
    // then i would be also very large. If i is of type "int", i*i is also "int". When i is 
    // very large, i*i would overflow. Therefore we should declare i as "long".  
    long i;
    for(i = 1; i < x; i++) {
        if(i*i > x) {
            break;
        }
    }
        
    return (int)i - 1;
}

A more efficient way is to use binary search:

public int mySqrt(int x) {
    if(x == 0 || x == 1) {
        return x;
    }
        
    int left = 1;
    int right = x; 
    while(left <= right) {
        long mid = left + (right - left) / 2;
        if(mid * mid == x) {
            return (int)mid;
        }else if(mid * mid > x) {
            right = (int)mid - 1;
        }else {
            left = (int)mid + 1;
        }
    }
        
    return right;
}

The process of the above code is like this: https://www.youtube.com/watch?v=hBAz_bDvWGk

---

9. Longest Consecutive Sequence

Given an unsorted array of integers, find the length of the longest consecutive elements sequence. Your algorithm should run in O(n) complexity.

Example:

Input: [100, 4, 200, 1, 3, 2]
Output: 4
Explanation: The longest consecutive elements sequence is [1, 2, 3, 4]. Therefore its length is 4.

As our algorithm should be in O(n), we can use hashtable to solve the problem:

import java.util.HashSet;
import java.util.Set;

public class LongestConsecutiveSequence {
    public int longestConsecutive(int[] nums) {
        if(nums.length == 0) {
            return 0;
        }

        Set<Integer> set = new HashSet<>();
        for (int num : nums) {
            set.add(num);
        }

        int result = 1;
        for (int num : nums) {
            int len = 1;
            if (!set.contains(num - 1)) {
                int lowerBound = num;
                while (set.contains(lowerBound + 1)) {
                    len++;
                    lowerBound++;
                }

                result = Math.max(len, result);
            }
        }

        return result;
    }
}

The process of the above code is like this: https://www.youtube.com/watch?v=iBcS_PBJTDE

---

10. Best Time to Buy and Sell Stock

Say you have an array for which the ith element is the price of a given stock on day i. If you were only permitted to complete at most one transaction (i.e., buy one and sell one share of the stock), design an algorithm to find the maximum profit. Note that you cannot sell a stock before you buy one.

Example 1:
Input: [7,1,5,3,6,4]
Output: 5
Explanation: Buy on day 2 (price = 1) and sell on day 5 (price = 6), profit = 6-1 = 5.
             Not 7-1 = 6, as selling price needs to be larger than buying price.


Example 2:
Input: [7,6,4,3,1]
Output: 0
Explanation: In this case, no transaction is done, i.e. max profit = 0.

Here is the code to solve the problem:

public class BestTime {
    public int maxProfit(int[] prices) {
        int profit = 0;
        int min = Integer.MAX_VALUE;
        for(int i = 0; i< prices.length; i++) {
            if(prices[i] < min) {
                min = prices[i]; 
            }
            profit = Math.max(profit, prices[i] - min);
        }
        
        return profit;
    }
}

day	0	1	2	3	4	5
price	7	1	5	3	6	4

If we are on day i, we can ask ourselves:

What is the maximum profit I can make today?

Firstly, we should check what is the minimum value before this day, then we subtract the minimum value using today’s price to get the maximum profit on day i. That’s why we should keep updating our min.

We can make our code more efficient:

public class BestTime {
    public int maxProfit(int[] prices) {
        int profit = 0;
        int min = Integer.MAX_VALUE;
        for(int i = 0; i< prices.length; i++) {
            if(prices[i] < min) {
                min = prices[i]; 
            }else {
                profit = Math.max(profit, prices[i] - min);
            }         
        }       
        return profit;
    }
}

---

11.LeetCode Problem: Pascal’s Triangle

In Pascal’s triangle, each number is the sum of the two numbers directly above it:

Given a non-negative integer numRows, generate the first numRows of Pascal’s triangle. For example, if numRows = 5, we get the following result:

[
     [1],
    [1,1],
   [1,2,1],
  [1,3,3,1],
 [1,4,6,4,1]
]

We can firstly observe the above result. We can easily find the following pattern for a particular row i:

1. There are always i elements in row i.
2. The first element and the last element are always 1.
3. The jth element in row i is the sum of j-1th element and jth element in row i-1.

For example, for row 4(i.e., [1,3,3,1]), we can find that:

1. There are 4 elements in total.
2. The first element and the last element are 1.
3. The 2nd element 3 is the sum of the 1st and 2nd element in row 3, namely, 3 = 1 + 2.

Here is the code to solve the pascal’s triangle problem:

import java.util.ArrayList;
import java.util.List;

public class PascalTriangle {
    public static List<List<Integer>> generate(int numRows) {
        List<List<Integer>> result = new ArrayList<>();

        // Handle the case numRows = 0
        if (numRows == 0) {
            return result;
        }

        // Handle the case numRows = 1
        List<Integer> row_1 = new ArrayList<>();
        row_1.add(1);
        result.add(row_1);

        // Handle the case numRows >= 2,
        // we start from the 2nd row.
        List<Integer> pre_row = result.get(0);
        for (int i = 2; i <= numRows; i++) {
            List<Integer> row_i = new ArrayList<>();
            row_i.add(1);// The first element is always 1.

            for (int j = 1; j < i - 1; j++) {
                row_i.add(j, pre_row.get(j - 1) + pre_row.get(j));
            }

            row_i.add(1);// The last element is always 1.
            result.add(row_i);
            pre_row = row_i;// Update the previous row
        }

        return result;
    }

    // main method to test the generate method.
    public static void main(String[] args) {
        List<List<Integer>> result = generate(5);
        result.forEach(list -> System.out.println(list));
    }
}

---

12. Valid Parentheses

Given a string containing just the characters ‘(‘, ‘)’, ‘{‘, ‘}’, ‘[‘ and ‘]’, determine if the input string is valid. An input string is valid if:

• Open brackets must be closed by the same type of brackets.
• Open brackets must be closed in the correct order.

Note that an empty string is also considered valid.

Example 1:
Input: "()"
Output: true


Example 2:
Input: "()[]{}"
Output: true


Example 3:
Input: "(]"
Output: false


Example 4:
Input: "([)]"
Output: false


Example 5:
Input: "{[]}"
Output: true

We can use a stack to solve this problem:

public class ValidParentheses {
  
  public boolean isValid(String s) {
      Stack<Character> stack = new Stack<>();
      
      for(char c : s.toCharArray()) {
          if(c == '(' || c == '[' || c == '{') {
              stack.push(c);
          } else if (c == ')' && !stack.isEmpty() && stack.peek() == '(') {
              stack.pop();
          } else if (c == ']' && !stack.isEmpty() && stack.peek() == '[') {
              stack.pop();
          } else if (c == '}' && !stack.isEmpty() && stack.peek() == '{') {
              stack.pop();
          } else {
              return false;
          }
      }
      
      return stack.isEmpty();      
    }
}

---

13. Counting Bits

Given a non negative integer number num. For every numbers i in the range 0 ≤ i ≤ num calculate the number of 1’s in their binary representation and return them as an array.

Example 1:
Input: 2
Output: [0,1,1]

---------------------

Example 2:
Input: 5
Output: [0,1,1,2,1,2]

Here is the code to solve this problem:

public class CountingBits {
    public int[] countBits(int num) {
        int[] result = new int[num + 1];
        
        result[0] = 0;
        for(int i = 1; i<= num; i++) {
            if(i % 2 == 0) { // even number
                result[i] = result[i/2];
            } else { // odd number
                result[i] = result[i/2] + 1;
            }
        }
        return result;
    }
}

Here is the explanation of the above code:

Given an even number, say 8, which is 1000 in binary, if we divide 8 by 2, all digits need to shift one place to the right:

       8/2 ==> 4
1000 >> 1  ==> 0100

As shown, since the last digit of an even number is always 0, the number of 1’s in 8 is same as the number of 1’s in 8/2.

Given an odd number, say 7, which is 0111 in binary, if we divide 7 by 2, all digits need to shift one place to the right:

       7/2 ==> 3
0111 >> 1  ==> 0011

As shown, since the last digit of an odd number is always 1, the number of 1’s in 7 is one more than the number of 1’s in 7/2.

---

14. Queue Reconstruction By Height

Suppose you have a random list of people standing in a queue. Each person is described by a pair of integers (h, k), where h is the height of the person and k is the number of people in front of this person who have a height greater than or equal to h. Write an algorithm to reconstruct the queue. For example:

Input:
[[7,0], [4,4], [7,1], [5,0], [6,1], [5,2]]

Output:
[[5,0], [7,0], [5,2], [6,1], [4,4], [7,1]]

Here is the code to solve this problem:

import java.util.*;

public class QueueReconstruction {
    public int[][] reconstructQueue(int[][] people) {
        if (people.length == 0) {
            return people;
        }

//        Arrays.sort(people, new Comparator<int[]>() {
//            public int compare(int[] a, int[] b) {
//                if (b[0] == a[0]) {
//                    return a[1] - b[1];
//                }
//                return b[0] - a[0];
//            }
//        });
        Arrays.sort(people, (a, b) -> (b[0] == a[0] ? a[1] - b[1] : b[0] - a[0]));

        ArrayList<int[]> list = new ArrayList<>();
        for (int i = 0; i < people.length; i++)
            list.add(people[i][1], new int[]{people[i][0], people[i][1]});

        int[][] result = new int[people.length][2];
        int i = 0;
        for (int[] person : list) {
            result[i][0] = person[0];
            result[i++][1] = person[1];
        }

        return result;
    }

}

The idea of the above code is shown in the following video: https://www.youtube.com/watch?v=z4FdQNfpyuM

---

15. Daily Tempretures

Given a list of daily temperatures T, return a list such that, for each day in the input, tells you how many days you would have to wait until a warmer temperature. If there is no future day for which this is possible, put 0 instead.

For example, given the list of temperatures T = [73, 74, 75, 71, 69, 72, 76, 73], your output should be [1, 1, 4, 2, 1, 1, 0, 0].

An efficient way to solve this problem is to use stack:

public class Solution {
    public int[] dailyTemperatures(int[] T) {
        int[] ans = new int[T.length];
        Stack<Integer> stack = new Stack();
        for (int i = T.length - 1; i >= 0; --i) {
            while (!stack.isEmpty() && T[i] >= T[stack.peek()]) {
                stack.pop();
            }
            ans[i] = stack.isEmpty() ? 0 : stack.peek() - i;
            stack.push(i);
        }
        return ans;
    }
}

And here is a good video explanation: https://www.youtube.com/watch?v=WGm4Kj3lhRI