Game Theory

There are two kinds of strategic interactions:

1. sequential: The players take actions in turn, e.g., playing chess.

2. simultaneous: The players act at the same time, in ignorance of the others’ current actions, e.g., prisoners’ dilemma.

Sequential Move Game

For sequential move games, we can follow the rule:

Look forward and reason backward.

Each player should figure out the other players’ future responses and use them in calculating his own best current move.

A game tree can help us to look forward and reason backward. Let’s look at the following example:

Lucy holds a football on the ground and invites Charlie to run up and kick it. At the last moment, Lucy pulls the ball away. Charlie, kicking only air, lands on his back, and this gives Lucy great perverse pleasure.

In this example, before taking any action, Charlie can draw a game tree like this:

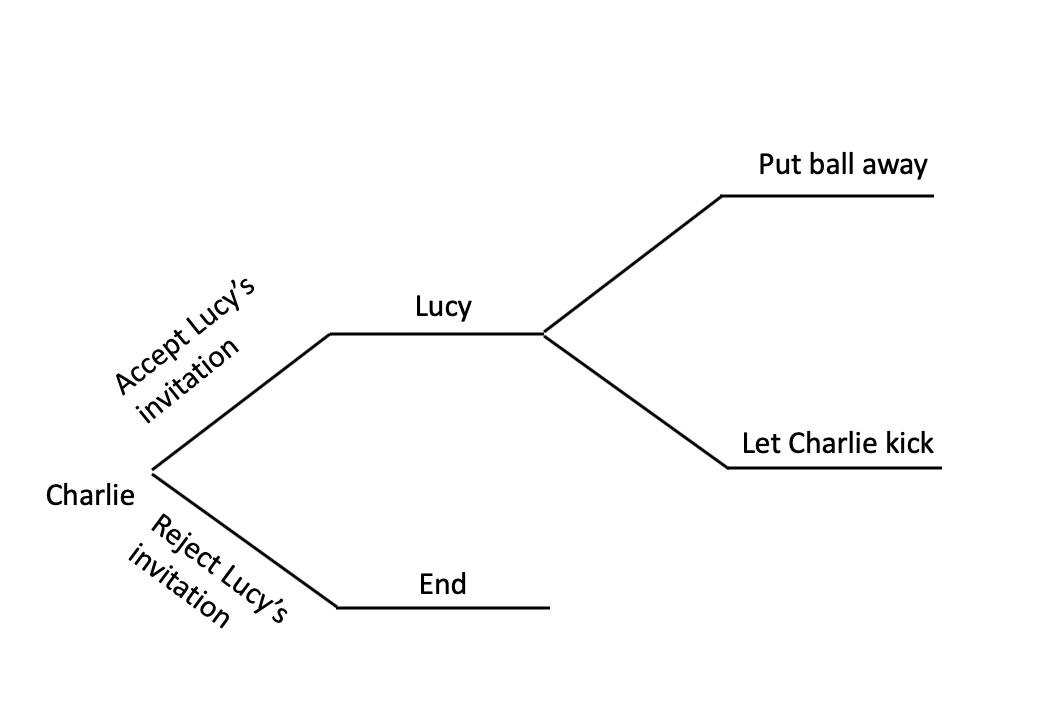
Based on other contexts, Charlie can know Lucy’s character and predict she will choose the upper branch. Therefore, Charlie should choose the lower branch:

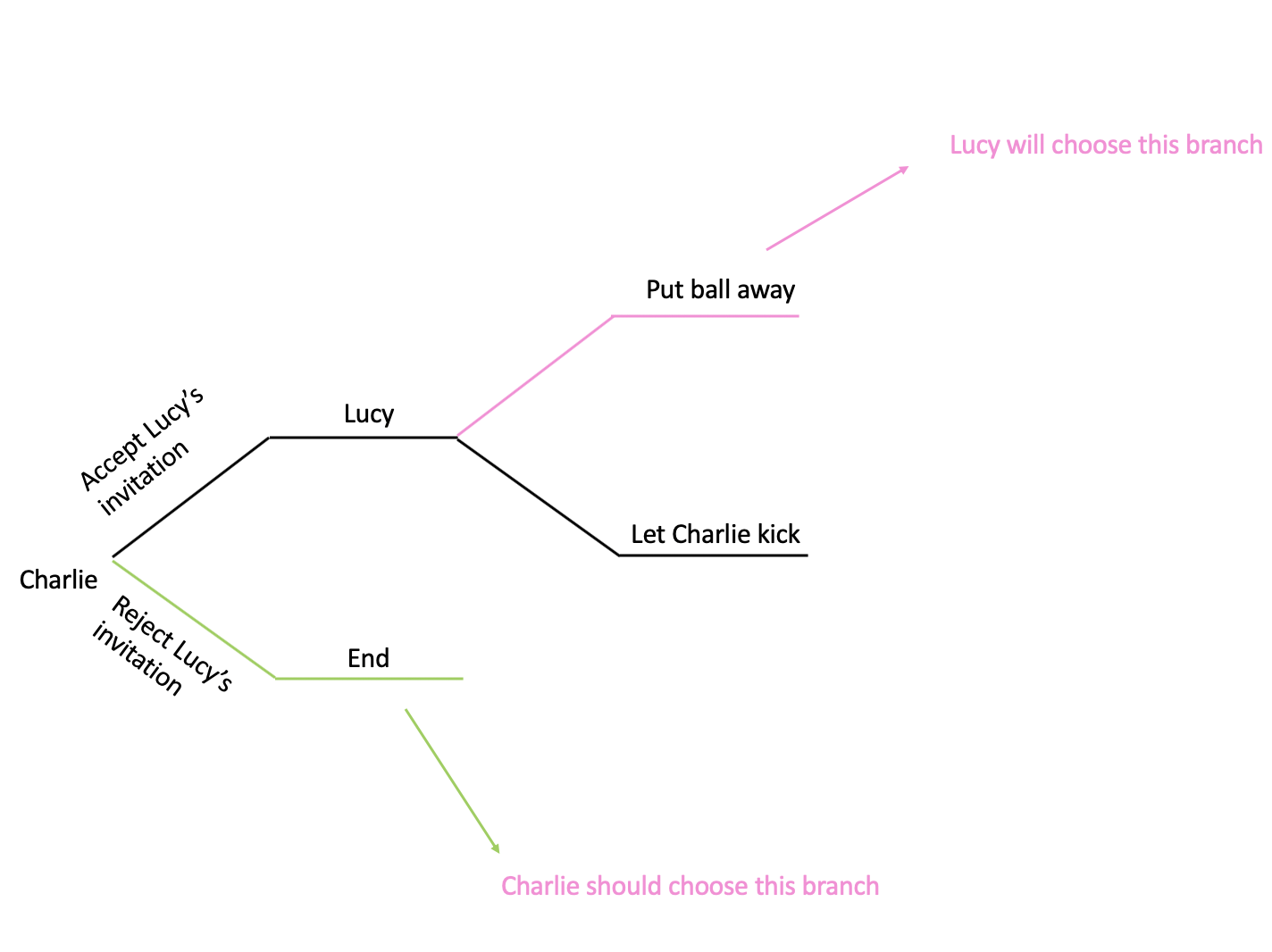
In real world, we can have more complex game trees, and in many cases we must face uncertainty about other players’ choices and make educated guesses on their choices.

---

Simultaneous Move Game

Prisoners’ Dilemmas

In real life, they are many instances of the prisoners’ dilemma. For example:

Two gas stations at the same corner, or two supermarkets in the same neighborhood, sometimes get into fierce price wars with each other.

In this case, if the gas station A charges a low price, the B station had better set its own price low to avoid losing too many customers; if A prices its gas high, B can divert many customers its way by pricing low. However, when both stations price low, neither makes money.

Without knowing each other’s choice, two stations take actions simultaneously. They all choose their best choice, however, the result is disappointing. That’s why we call it dilemma.

To analysis the above simultaneous move game, we can use a table to lay out all the combinations of the simultaneous choices two stations could make:

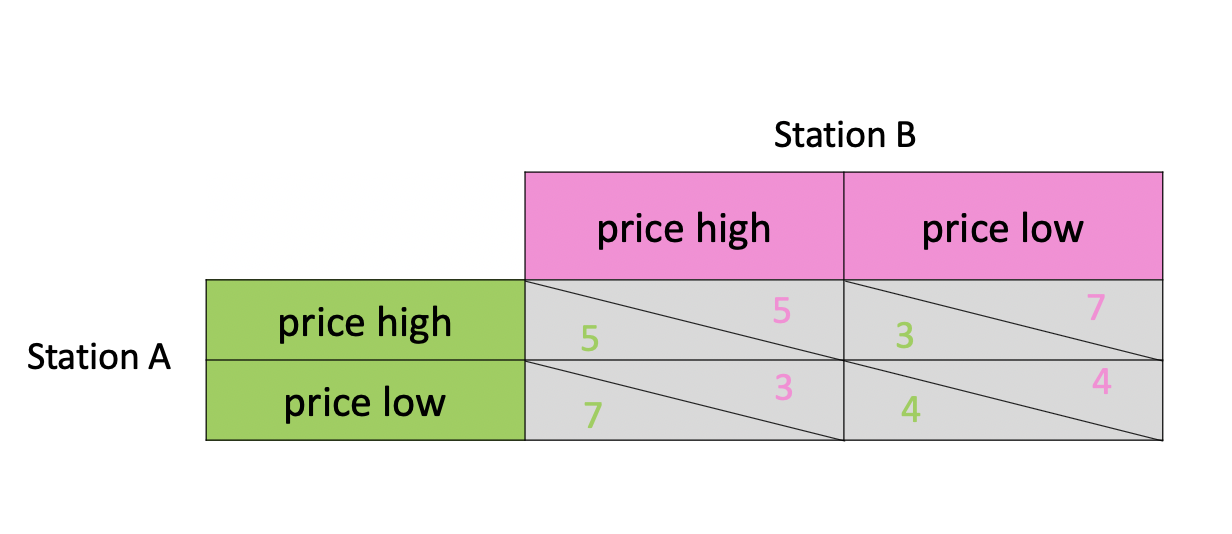
As shown, suppose we are station B:

• If station A choose high price, then we should choose low price.

• If station A choose low price, we should also choose low price.

For station B, no matter what choice station A would make, the better choice is always low price. Therefore, in this case, low price is station B‘s dominant strategy. And we should remember:

If you have a dominant strategy, use it.

In this case, station A‘s dominant strategy is also low price. The two stations both choose to low their prices, but they all makes less money(if they did not low their prices, they can earn 5, which is bigger than 4).

How to resolve the dilemma? In this gas station case, two stations can make agreements on keeping high price.

Basically, we should make sure the players have strong incentives to achieve cooperation. If they choose cooperation, they can recieve a reward. And if someone choose defection, he would be punished. This need players design reward/punishment in advance.

Nash Equilibrium

One evening, two hunters meet at a campfire party. They have a talk with each other and realise that:

• By cooperating they could hunt bigger animals, such as stag or bison.

• One person on his own cannot expect any success hunting either stag or bison.

Therefore, they decide to go hunting together the following day. However, in the next morning, they both have forgotten whether they decided to go after stag or bison. The hunting grounds for the two species are in opposite directions. There were no cell phones, and they have to make choices(stag or bison) in isolation.

Unlike prisoners’ dilemma, in this case two players do not have dominant strategies. In another word, hunter A‘s best choice depends on what Hunter B does, and vice versa. Each hunter has to think about the other’s choice and figure out his own choice. We can have a table like this:

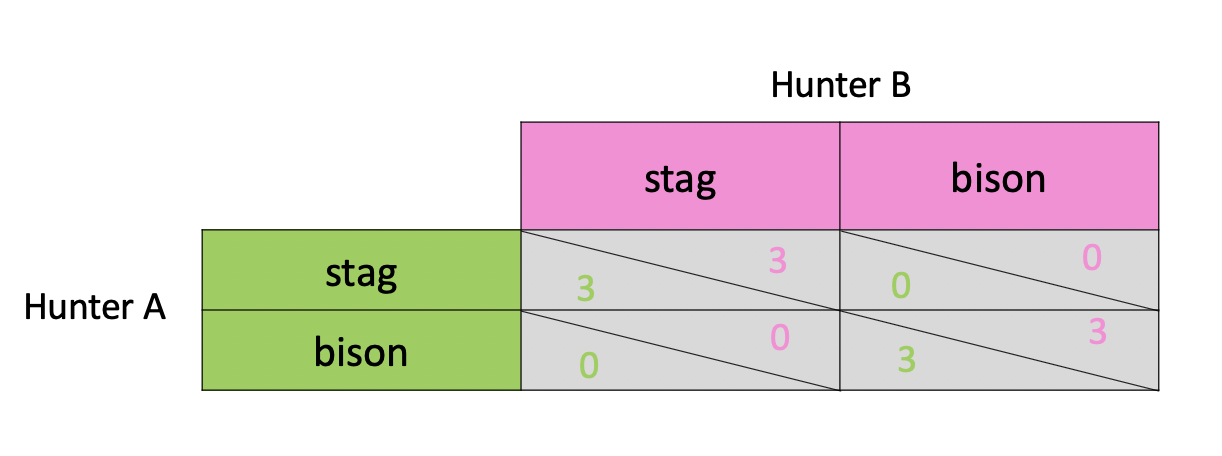
This game has two Nash equilibria:

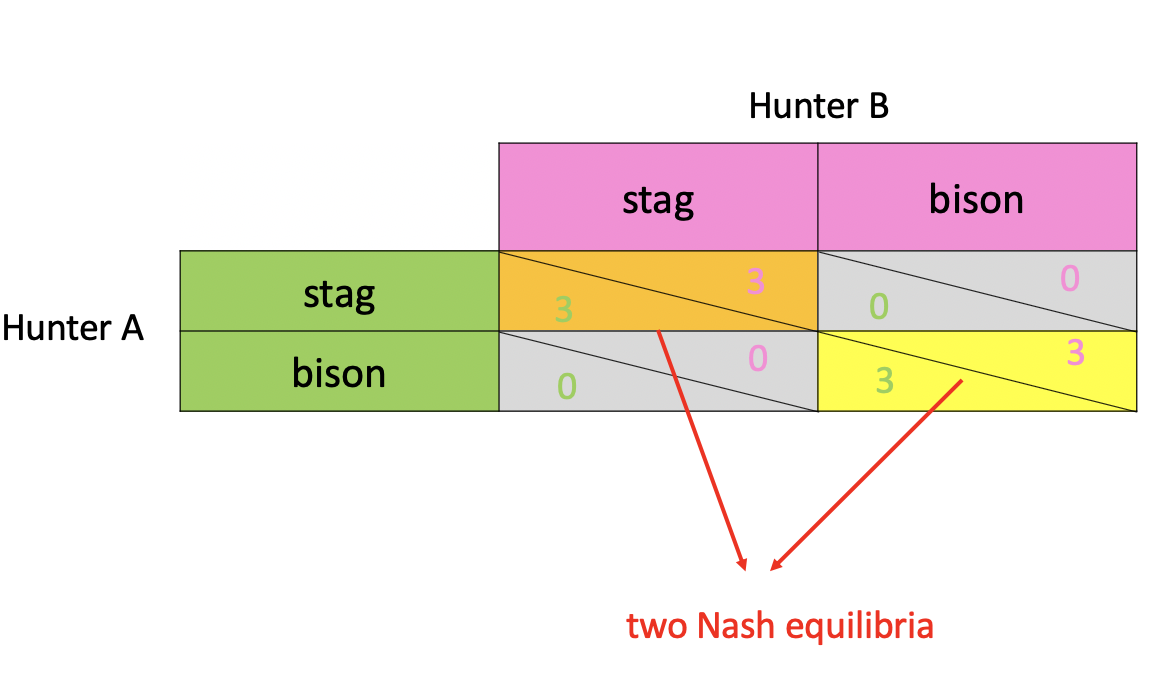
Which equilibrium the two hunters tend to achieve? To achieve one of these equilibria, the two hunters need to find the focal point.

What is focal point? Suppose each of two players is asked to choose a positive integer. If both choose the same number, both get a prize. If the two choose different numbers, neither gets anything. The overwhelmingly frequent choice is 1, because it is the first among the whole positive integers, it is the smallest. Therefore, 1 the is focal point in this case.

Back to our hunting problem, if during the two hunters’ talk, they both agree that stag is more delicious than bison, their focal point could be stag. The focal point can help them make the right choice.

Chicken Game & Battle of the Sexes

Chicken game is a classic game:

Two people drive toward each other on a straight road, and the first one to swerve to avoid a collision is the loser, or chicken. If both keep straight, however, they crash, and that is the worst outcome for both.

For this game, we can have a playoff table like this:

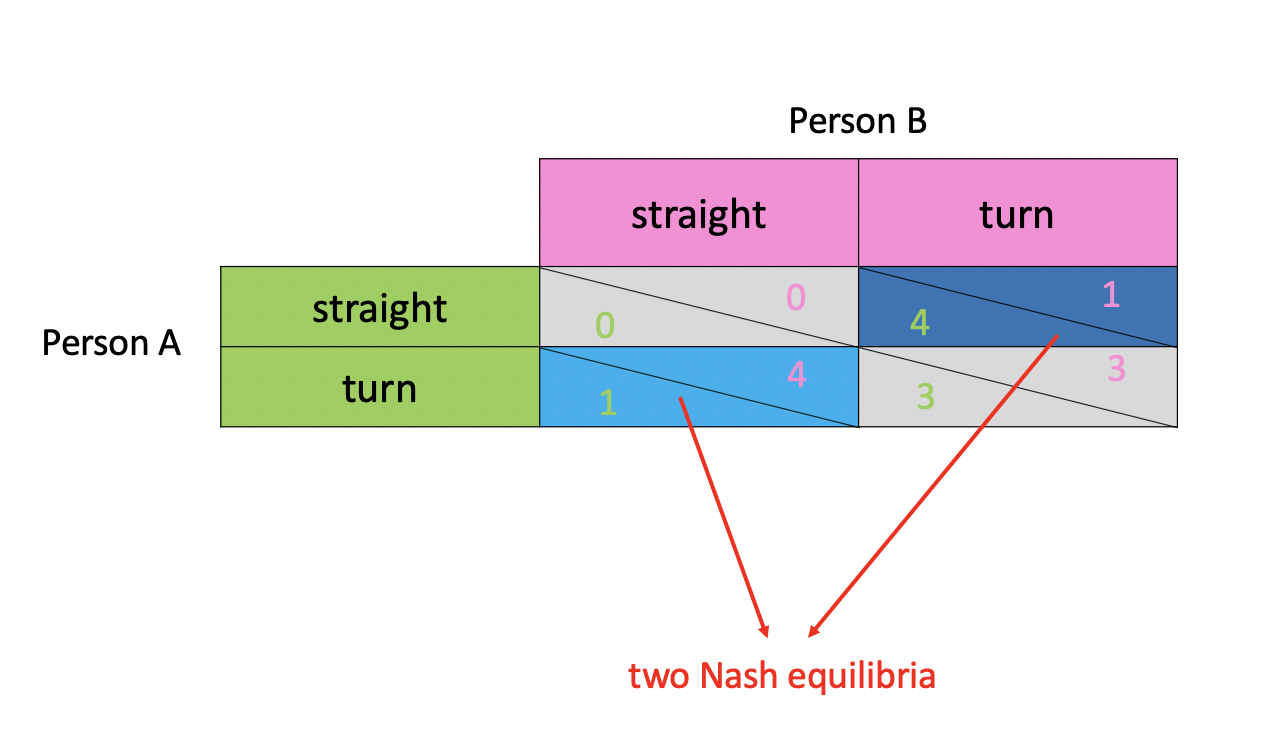
Note that we have two Nash equilibria here, but each person wants to achieve his preferred equilibrium.

To solve this problem, one of the players, say person A, may make a commitment to choosing his preferred strategy, namely going straight. It is important to make this commitment credible and to ensure that the other player knows it.

Let’s look at a similar game, i.e., battle of the sexes:

A husband and wife have different preferences in movies, and the two available choices are very different. 

The husband wants to see '300'. The wife likes 'A Beautiful Mind'. 

But both prefer watching either movie in the other’s company to watching any movie on their own.

For this problem, we can have the following table:

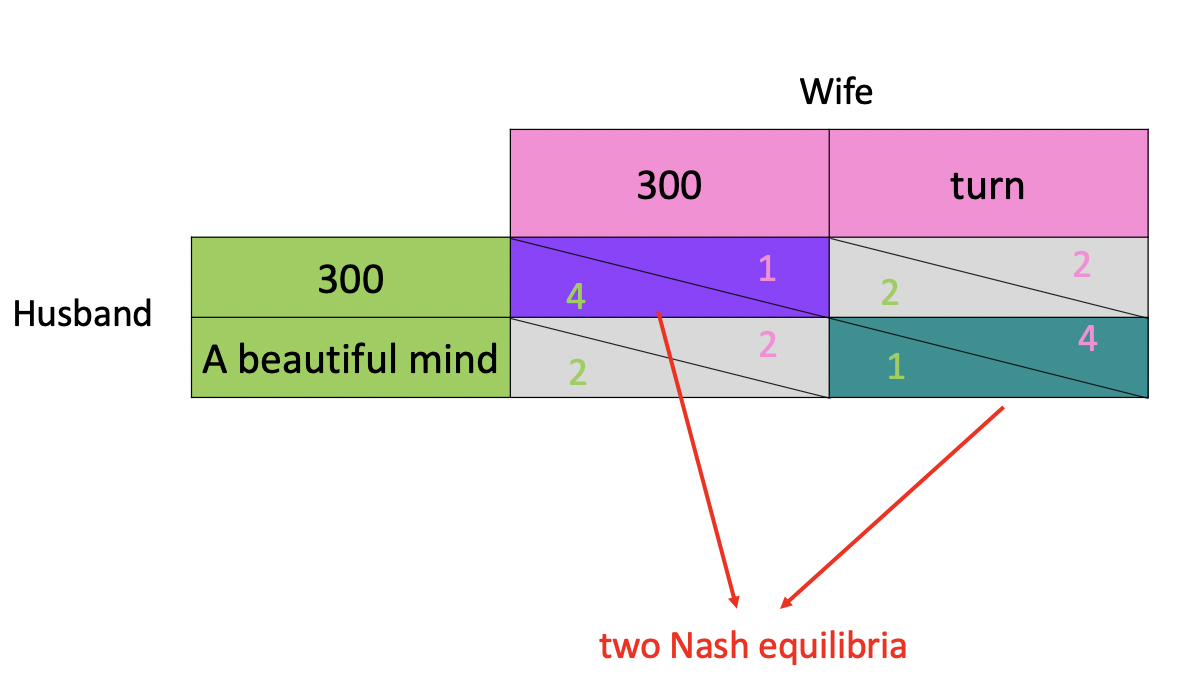
Like the chicken game, one of the couple can make a commitment to insist his/her choice. In this way, he/she can force the other to accept his/her choice.

However, the conflict in this game is not as sharp as in chicken game. And the husband and wife will live together for a long time.Therefore, this time, they can make decision based on the wife’s preference, and next time the husband’s preference…