Amortized Complexity

algorithm

Amortized Complexity

Amortized time complexity considers the overall effect of a set of operations. One typical example used to demonstrate amortized time complexity is the dynamic array.

Suppose we have an empty array:

amortized_complexity_1

Now we want to insert an unknown number of elements into this array. When the array gets full, we need to create a new array that is double the size, and copy everything into this new array:

amortized_complexity_2

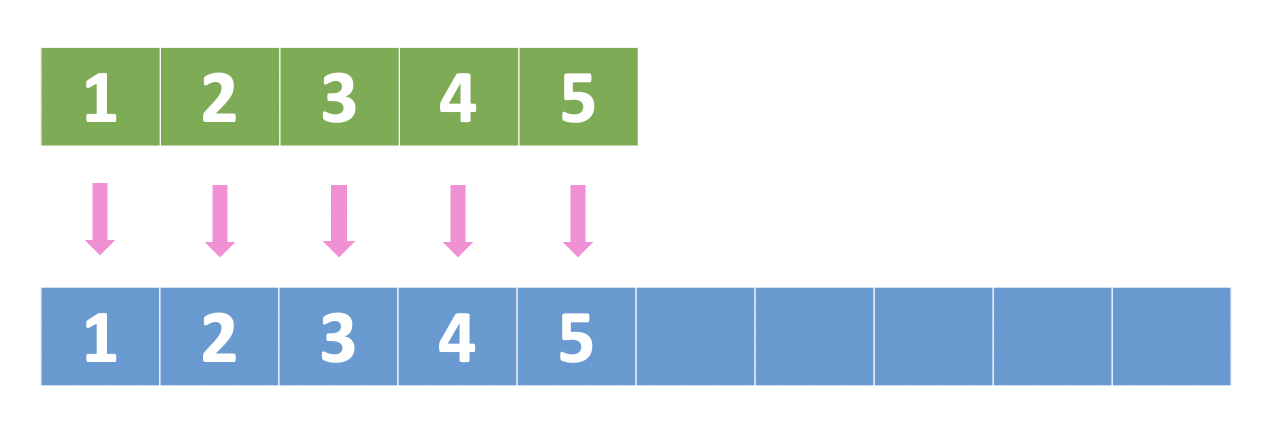
Next time when the array gets full again, we create a double-sized array again and copy everything into this new array…

When we insert an element that does not trigger an array expansion, the time complexity is just O(1):

amortized_complexity_3

However, when we insert an element that triggers an array expansion, we need to copy n items into a new array, which is in O(n):

amortized_complexity_4

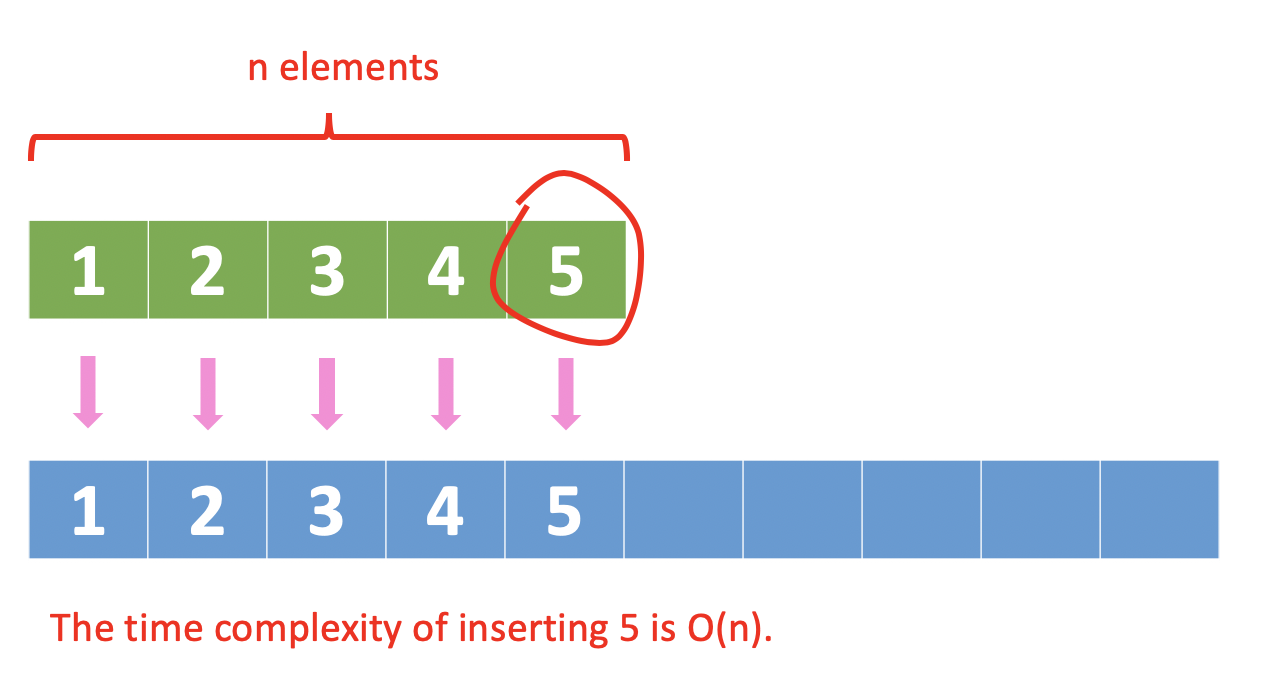
So, for a dynamic array, what is the real time complexity of insertion? In this case, we use amortized time complexity.

As mentioned above, we create an empty array, which can contain 5 elements. Each time the array becomes full, we double its size and do the copy. For simplicity, assume we want to insert n = 5 * 2^k elements into this array, the process would be:

1
2
3
4
5
6
7
8
             5 insertions    (initial size: 5)
5 copies  +  5 insertions    (size: 10)
10 copies +  10 insertions   (size: 20)
20 copies +  20 insertions   (size: 40)
40 copies +  40 insertions   (size: 80)
......

We have k rows(not including the first row) here.

We have 5 + 5 * (1 + 2 + 4 + ... + 2^k-1) insertions(because 1 + 2 + 4 + ... + 2^k-1 = 2^k - 1, we can know that 5 + 5 * (1 + 2 + 4 + ... + 2^k-1) = 5 * 2^k = n), and 5 * (1 + 2 + 4 + ... + 2^k-1) copies. Therefore we have 5 + 2 * 5 * (1 + 2 + 4 + ... + 2^k-1) operations in total. Then we can calculate the amortized cost of inserting n elements:

1
2
amortized cost = 5 + 2 * 5 * (1 + 2 + 4 + ... + 2^k-1) ➗ n 
               = 5 + 2 * 5 * (1 + 2 + 4 + ... + 2^k-1) ➗ 5 * 2^k

This is quite understandable. Indeed, inserting 5 * 2^k elments into a dynamic array costs 5 + 2 * 5 * (1 + 2 + 4 + ... + 2^k-1) operations.

Then we can obtain the amortized time complexity, which is θ(1), or O(1).

In Java, ArrayList is actually resizable array, and it uses a growth policy. Each time the ArrayList becomes full, its capacity grows automatically. And similarly, ArrayList.add has constant amortized time complexity(i.e., O(1)).