Uninformed Search Strategies

algorithm

Uninformed Search Strategies

Why We Need Search: Problem Formulation

Given initial state, the process of looking for a sequence of actions that reaches the goal state is called search:

1
2
             a sequence of actions
intial state ====================> goal state

Each action has a cost, and the sum of all the actions’ costs is the cost of the solution, i.e.,

cost of the solution = sum of the costs of the actions

In summary, search algorithms search for solutions to a given problem:

  • Input: problem formulation
  • Output: solution, i.e., a sequence of actions that minimize/maximize the cost

Uninformed search is also called blind search. Uninformed search strategies/algorithms have no information about states beyond that provided in the problem definition. All they can do is to generate child nodes and distinguish a goal state from a non-goal state.

According to which frontier node to visit first, we can divide uniformed search strategies into two types, i.e., breadth-first search and depth-first search. Breadth-first and depth-first search are techniques that can be used when the cost of each action is the same.

For breadth-first search, the root node is expanded first, then all child nodes of the root node are expanded next, then their child nodes, and so on. Breadth-first search is a level-by-level strategy, which means that all the nodes are expanded at a given depth in the search tree before any nodes at the next level are expanded.

Let’s look at an example of breadth-first search:

breadth_first_1

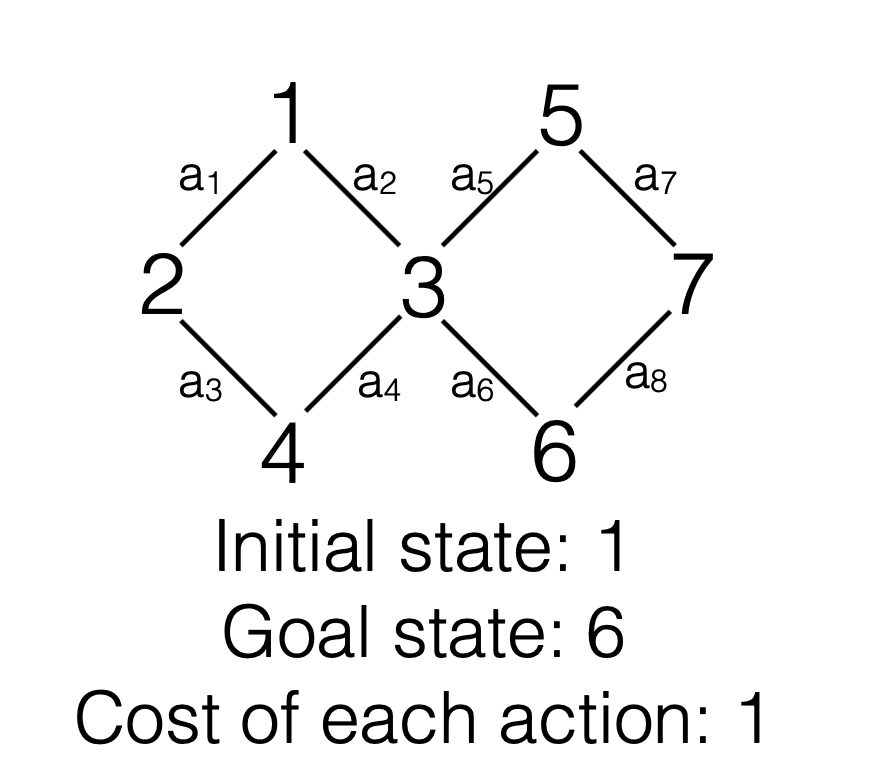
In the above graph, we want to find the shortest path from the initial state to the goal state. The cost of each action is the same(a1 = a2 = a3 = a4 = a5 = a6 = 1). Now we build the search tree for this example, at the same time, we use a FIFO queue for the frontier:

breadth_first_2

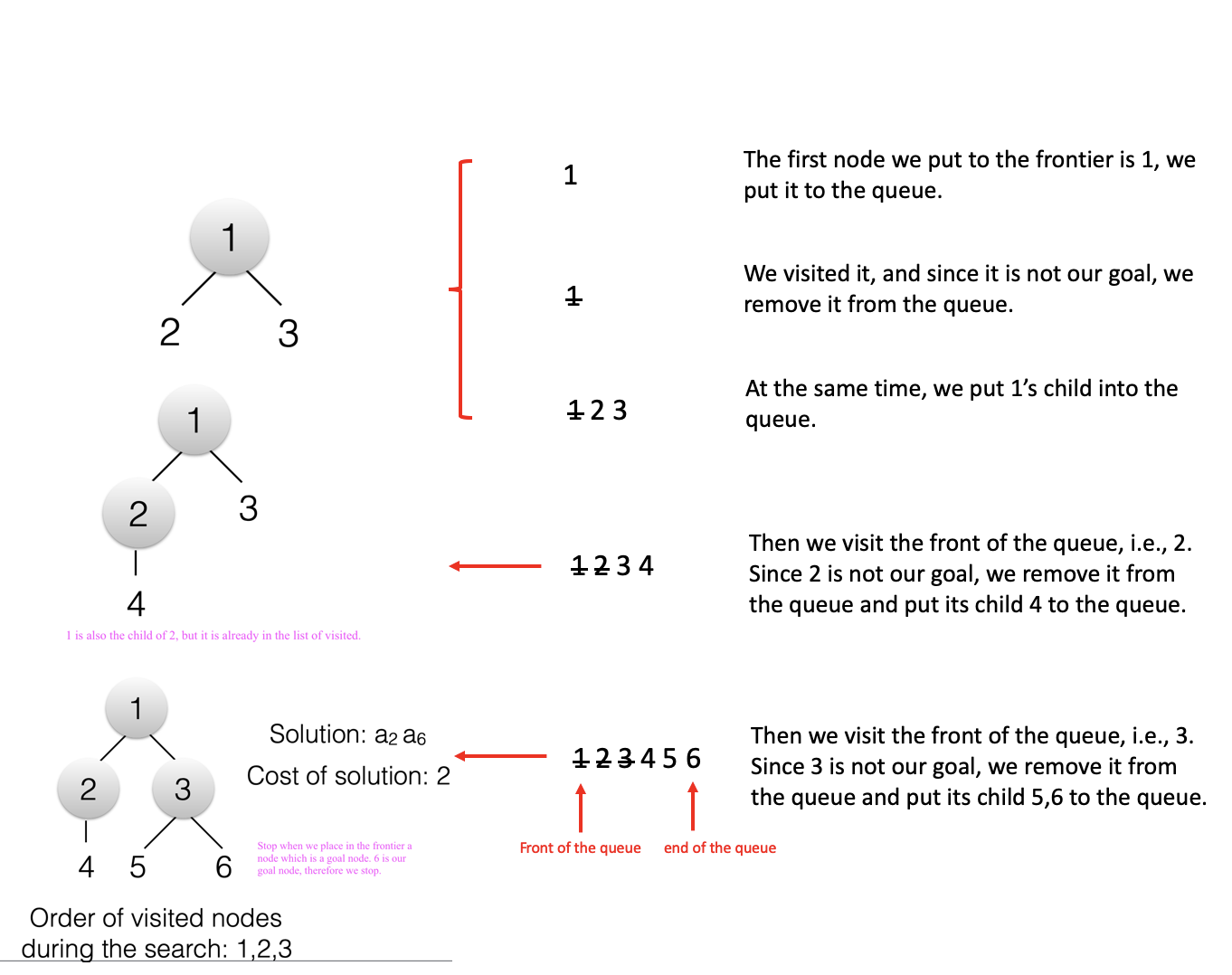
From the above example, we can conclude the properties of breadth-first search:

breadth_first_3

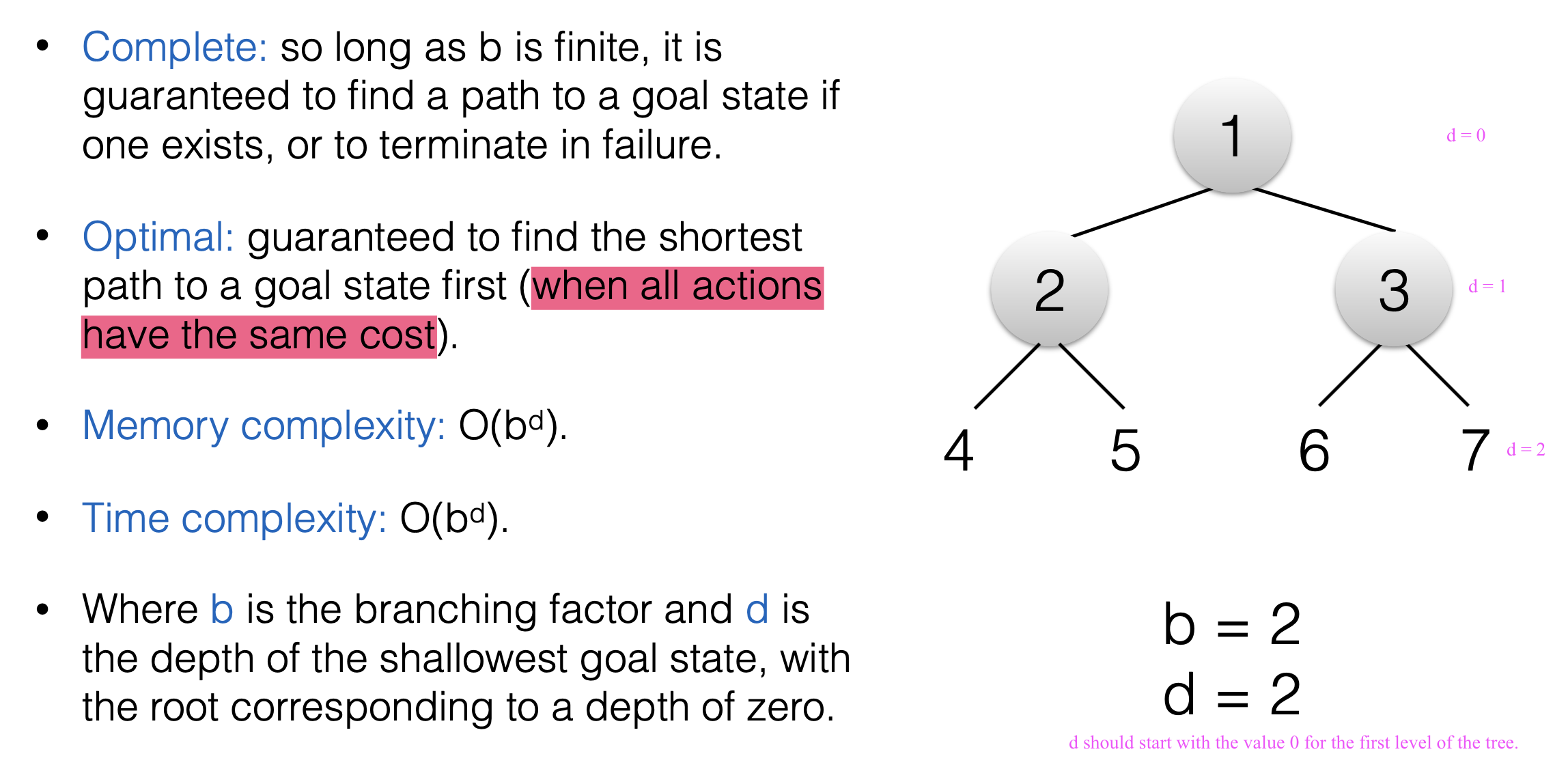
The time complexity of breadth-first search is O(b^d), where b is the branching factor and d is the depth of the shallowest goal state. Let’s look at a simple case:

breadth_first_4

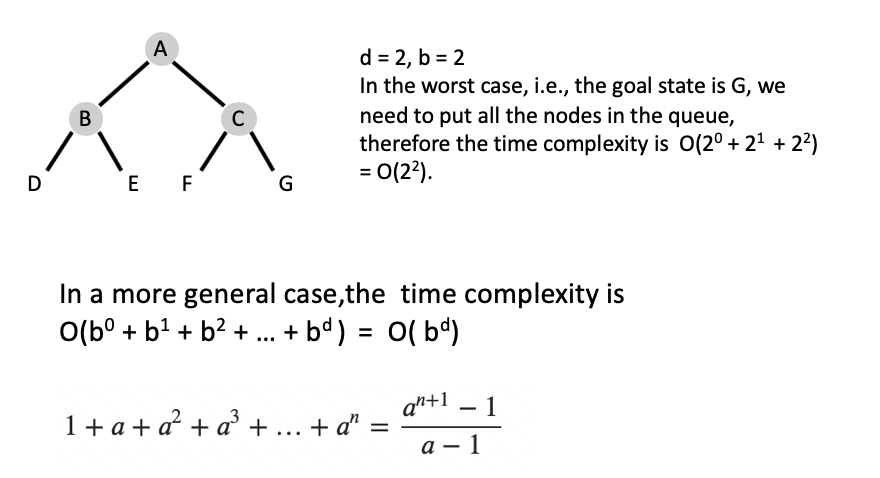
Similarly, in the worst case, we need to build and maintain a tree with all the nodes, therefore the space complexity of breadth-first search is also O(b^d).

Another thing I want to point out is that breadth-first search is not optimal when different actions have different costs. For example, suppose we have a graph like this:

breadth_first_5

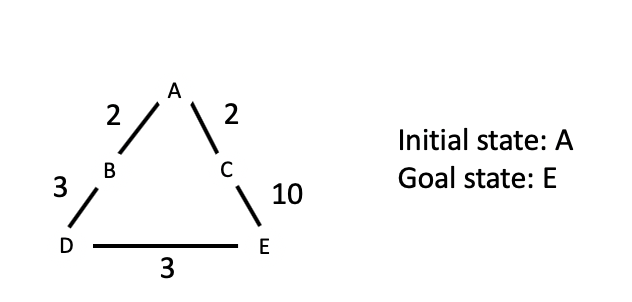
Now we want to go from A to E, if we use breadth-first search, the path would be:

breadth_first_6

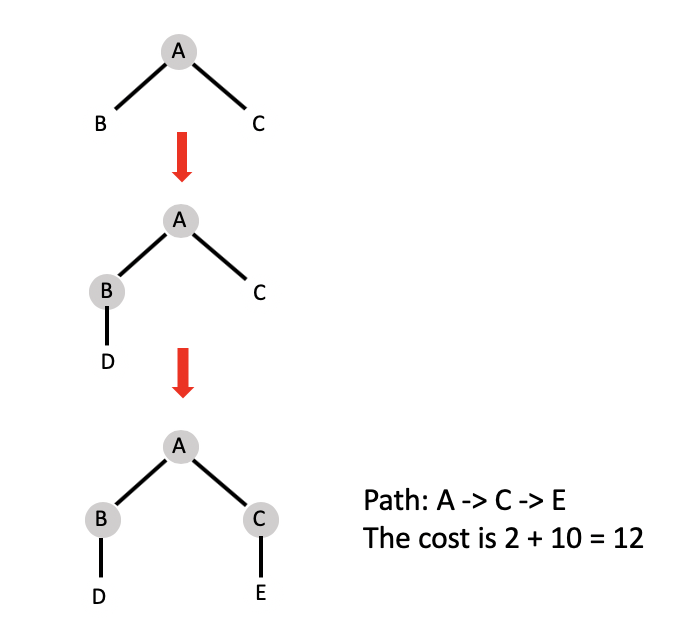
However, the solution is not optimal, since we can find a path that costs less, i.e., A -> B -> D -> E, the cost is 8.

Depth-first search always expands the deepest node in the current frontier of the search tree. And it uses a LIFO queue(i.e., stack). Suppose we have a graph like this:

depth_first_1

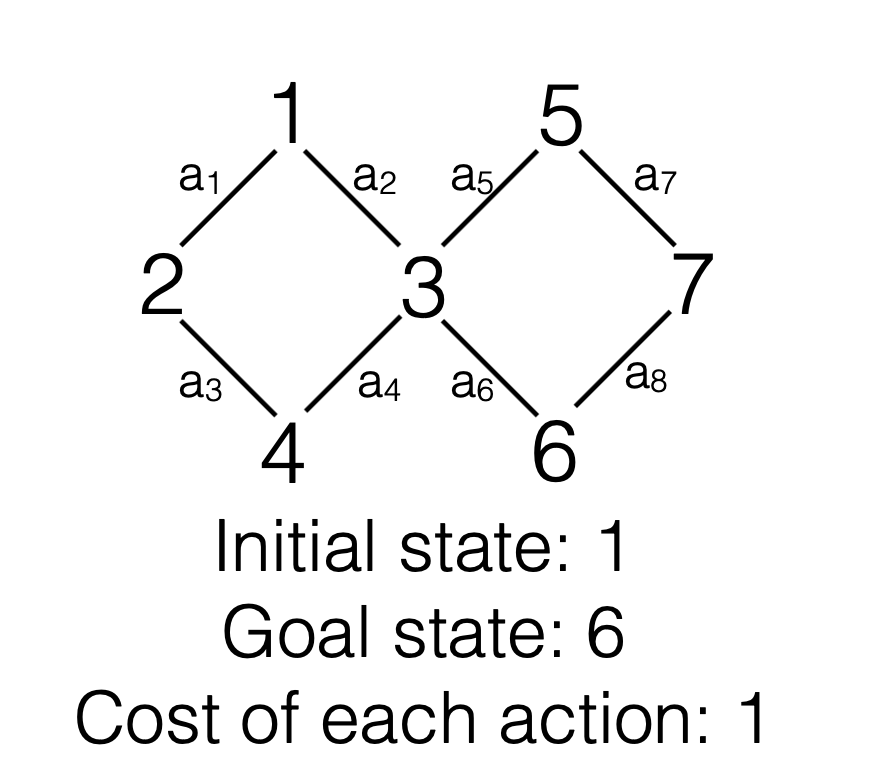
We can find the goal state like this:

depth_first_2

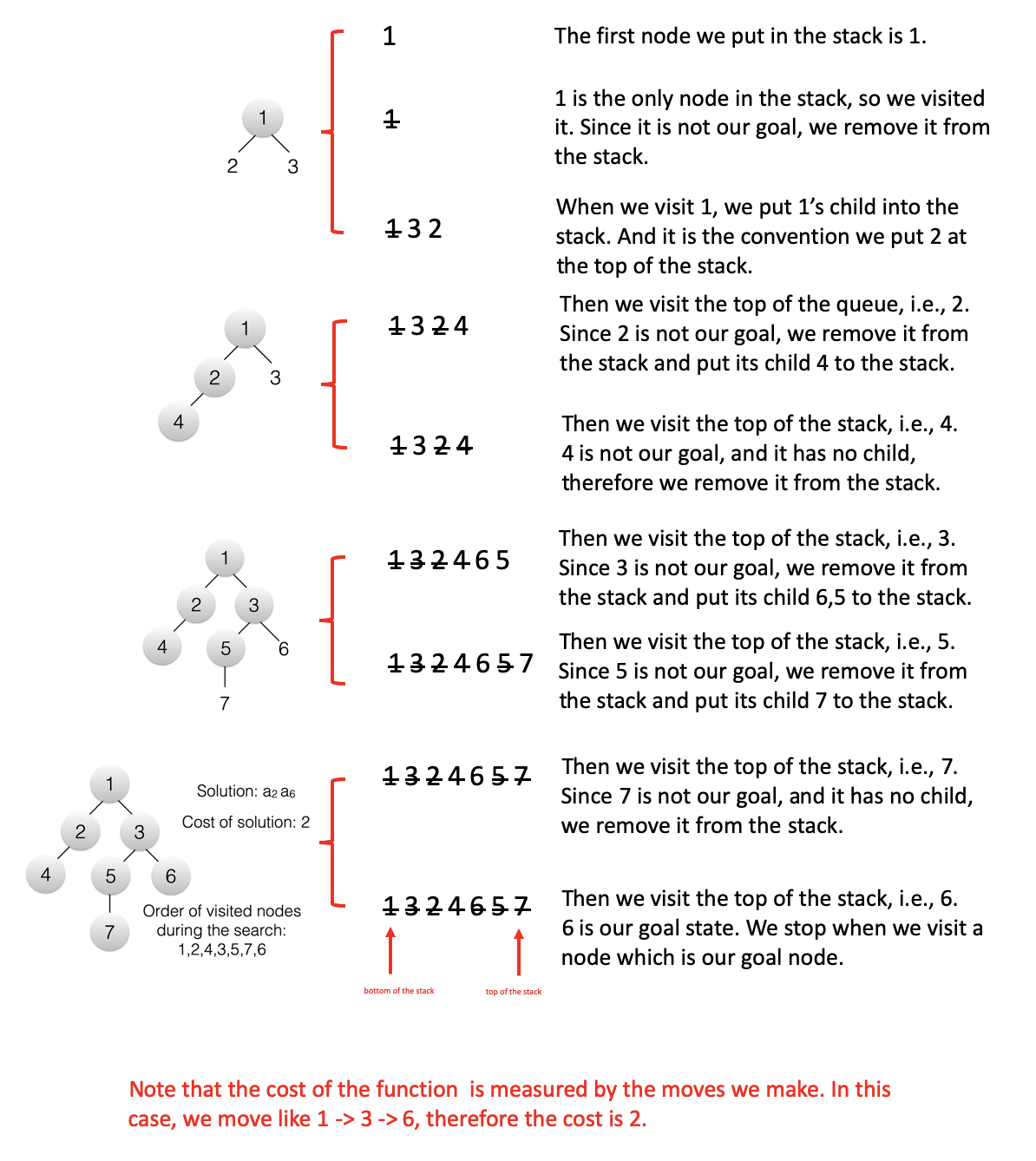
For the above example, we can conclude the properities of depth-first search:

depth_first_3

The time complexity and space complexity of breadth-first search are O(size of state space)(i.e., the size of the state space graph), since we need to put all the nodes onto the stack in the worst case. We must be careful here, since O(size of state space) basically means that the depth-first search algorithm grows linearlly with the size of the state space graph, but the state space graph itself can be potentially very large. The size of state space may go exponentially, just like the above example.

Depth-first search is not optimal. For example, in the following picture, depth-first search will explore the entire left subtree even if node C is a goal node. If node J were also a goal node, then depth-first search would return it as a solution instead of C, which would be a better solution; hence, depth-first search is not optimal.

depth_first_4

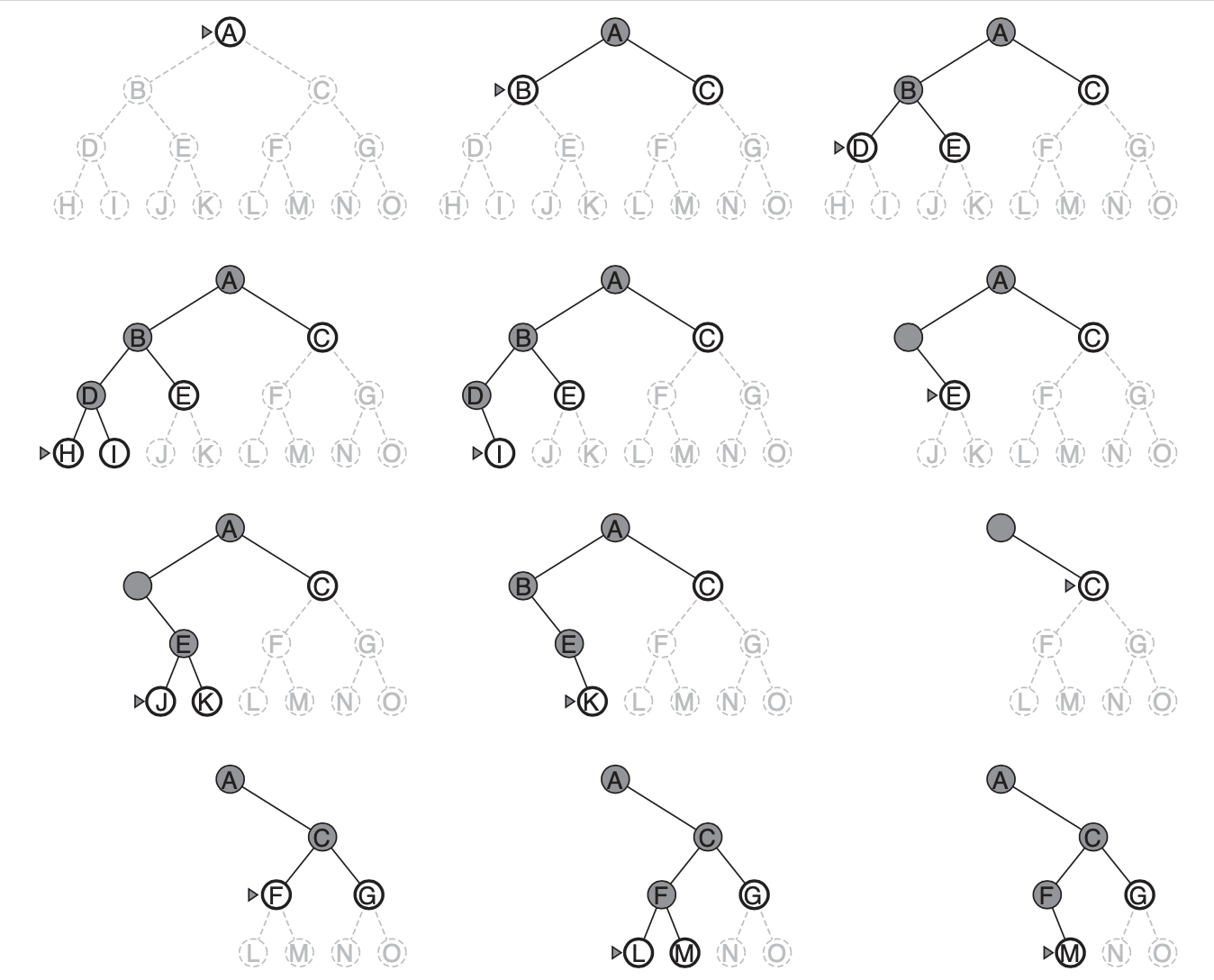
By now, depth-first search seems to have no clear advantage over breadth-first search. Indeed, for a graph search, there is no advantage. However, for a depth-first tree search(we call this tree-search version of depth-first search), if we store only the nodes in the path from the root to the current node, we could save space. That is, as shown in the above picture, once a node has been expanded, it can be removed from memory as soon as all its descendants have been fully explored. For a state space with branching factor b and maximum depth m, depth-first search requires storage of only O(bm) nodes. In this case, b = 2, and as shown in the above picture, each level has at most 2 nodes.

To guarantee that the depth-first search will terminate (either in success or failure) in a reasonable amount of time, we can put a limit on the maximum search depth l. That is, nodes at depth l are treated as if they have no successors. This strategy is called depth-limited search.

For depth-limited search, if we choose l < d(d is goal’s depth), it would be incompete since the shallowest goal is beyond the depth limit. A search algorithm is complete if it is guaranteed to find a solution when at least one solution exists. In this case(l < d), the search will always terminate in failure, therefore it is incompete. In addition, the depth-limited search will also be non-optimal if we choose l > d.

The time complexity of depth-limited search is O(b^l) and the space complexity is O(bl).

Conclusion

uninformed_search