Block Cipher Modes

Block ciphers (such as DES and AES) can be used directly only for a single block of plaintext. However, typically we want to encrypt plaintext that is much longer than a single block. There are several block cipher modes to help us to this securely.

Electronic Codebook (ECB) Mode

ECB is the easist way to do block cipher, which applies the encryption/decryption block by block:

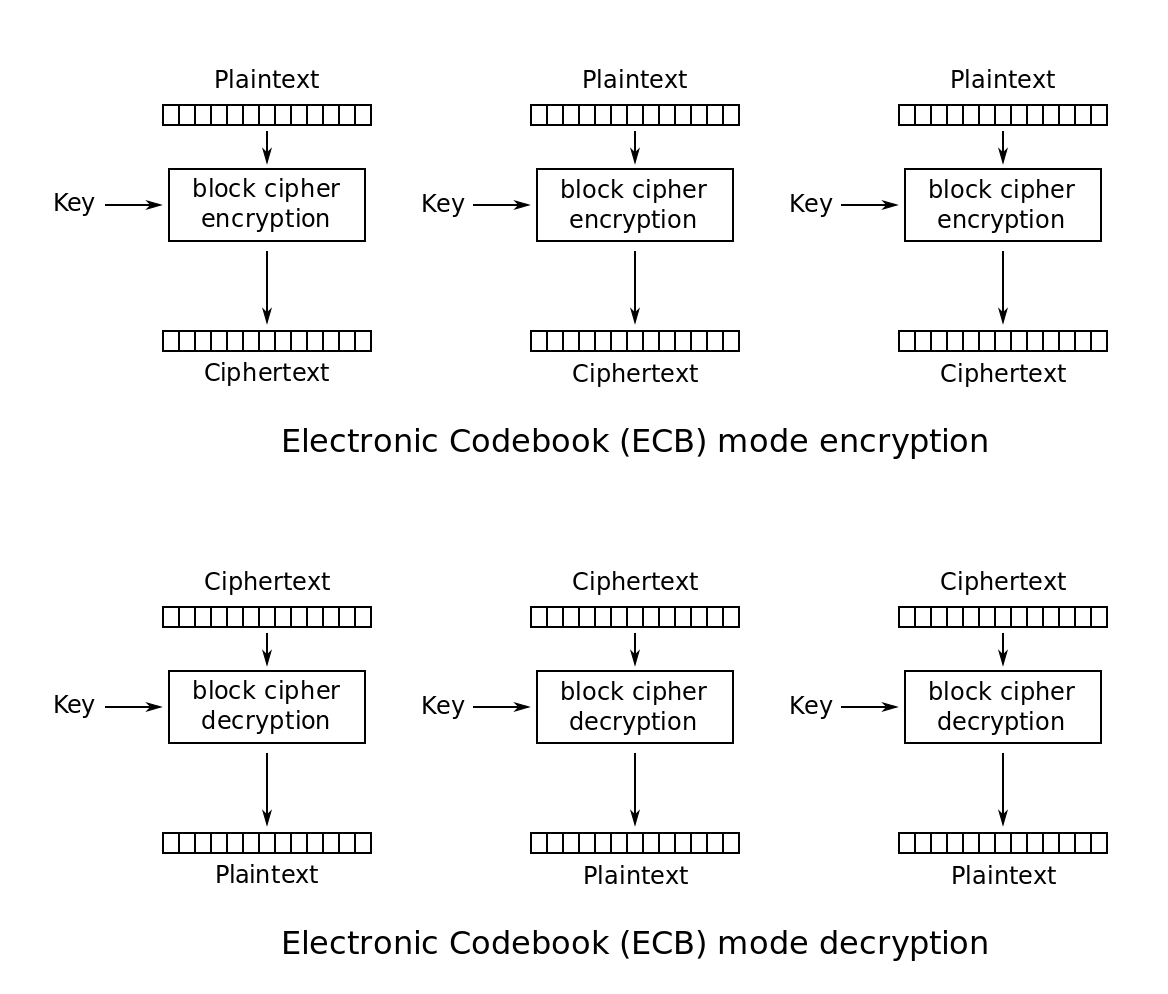
Cipher Block Chaining (CBC) Mode

CBC adds a random initialisation vector (IV) to randomise the first block, and then uses each block to randomise the next block. The encryption/decryption process is as below:

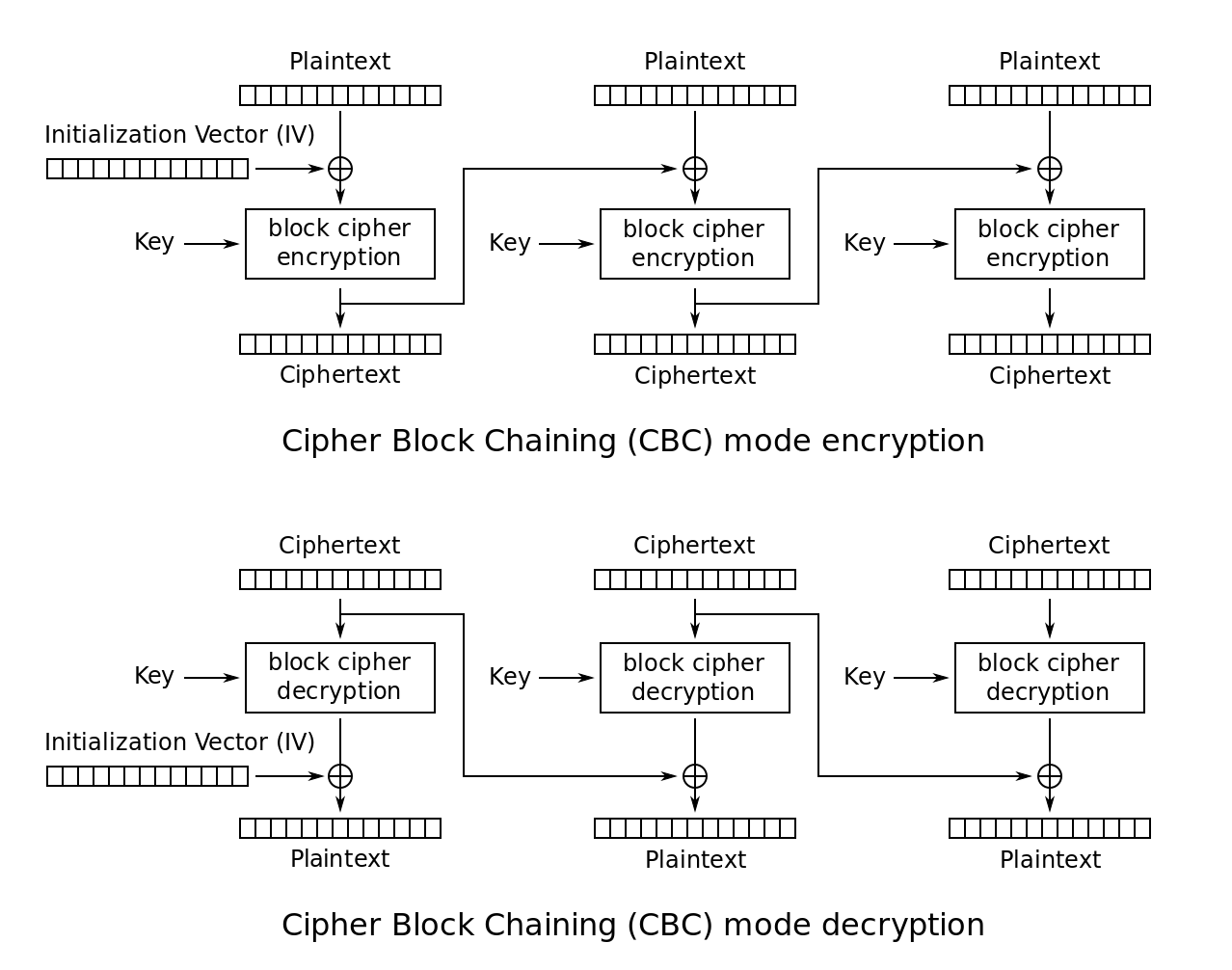
There are several things worth noting:

1. The IV should be randomly chosen for each encryption.
2. We must store the IV with the ciphertext, otherwise it’s not possible to decrypt. Thus, the IV is random, but not secret.
3. Since the ciphertext includes the IV, it is one block longer than the plaintext. So we have a small expansion in size.

Counter(CTR) Mode

To encrypt a message, we chose a random nonce(number used once), and then set up a counter which is incremented for each block:

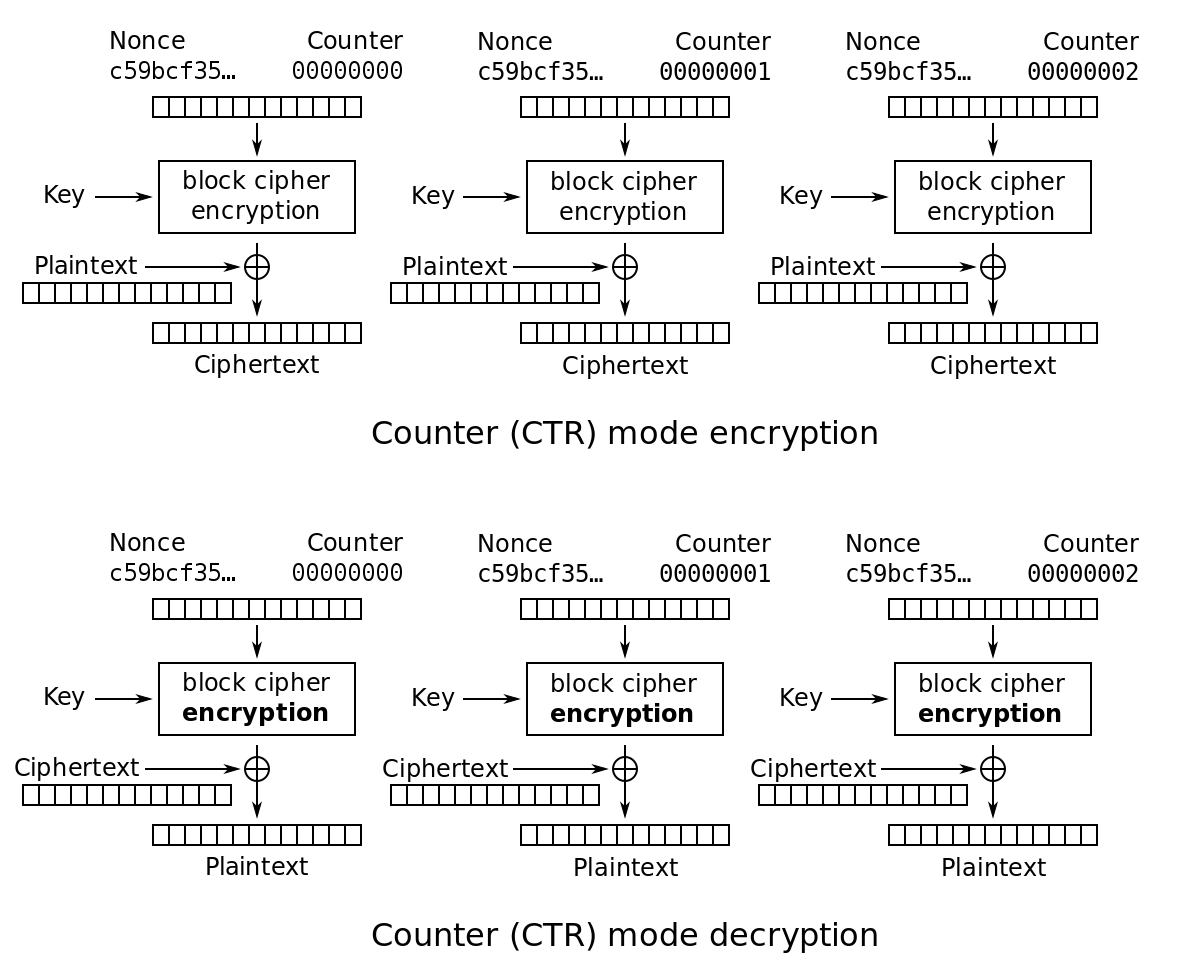
The nonce must be stored with or transmitted with the ciphertext blocks. Thus, similarly to the IV in CBC, in CTR mode the nonce must be chosen at random, but is not secret. Like CBC, CTR also increases the size of the ciphtertext by one block.

Indistinguishability Under Chosen-plaintext (IND-CPA) Game

Are the above block cipher modes really secure? We can play a IND-CPA game to verify the security. Here is the process of IND-CPA game:

IND-CPA gives the attackers a lot of power, i.e., they can do efficient operations (polinomial time). However, attackers cannot search through all keys, as the number of possible keys increases exponentially with the length of the key.

Does the attacker really win this game if b' = b? If we flip a coin, it is either head up or tail up, which means we have a 50% chance to guess the right answer. In this game, an attacker can also guess an answer, and the probability of winning is also 50%. Therefore, we should have a more precise way of defining how to win IND-CPA game:

Now we have figured out what is IND-CPA game and how to win this game. Then we can verify the security of block cipher by playing this game.

ECB is not secure

ECB is not secure, an attacker can easily win the IND-CPA game. For ECB mode, identical blocks within a plaintext always produce identical ciphertext blocks, which means we can easily distinguish the plaintext patterns:

For example(not very appropriate), to win the game, an attacker can send m0 and m1 like this:

m0: 1111111111111111
m1: 1234123412341234

We know that m0 and m1 follow different patterns, and their ciphertexts’ patterns must also be different. Therefore we can easily distinguish which one the challenger chose.

CBC and CTR are secure

Unlike ECB, in CBC and CTR we can not distinguish the plaintext patterns:

Therefore using CBC mode or CTR mode is secure.

However, there is a variation of CBC, which is not secure. In CBC, we should use a random IV each time. Here, we are simply incrementing the IV used last time, instead of taking a fresh random one:

Each time an encryption is done, the IV that is used is the previous IV plus 1.

This variation is insecure:

Consider what would happen if a counter, starting from zero, was used as an IV. Suppose the first message sent is 0000000000000000. The IV would be 0000000000000000, so the input to the block cipher is 0000000000000000. Now, suppose a second message 0000000000000001 is encrypted. This time, the IV is 0000000000000001, causing the input to the block cipher to be the same as before: 0000000000000000 (because 1 XOR 1 is 0).

In general, whenever the first plaintext block is equal to the IV, the result will always be the encryption of 0000000000000000. If the adversary knows this value, they can look at a given (IV, ciphertext) pair(IV is not secret!) and know whether or not the first block is the same as the IV. When the IV is random, it’s much less likely for the IV to coincide with the first plaintext block by accident.