Symmetric Crptography: Three Simple Ciphers

1. Columnar Transposition Cipher

Suppose we have a plaintext:

To be or not to be, that is a question.

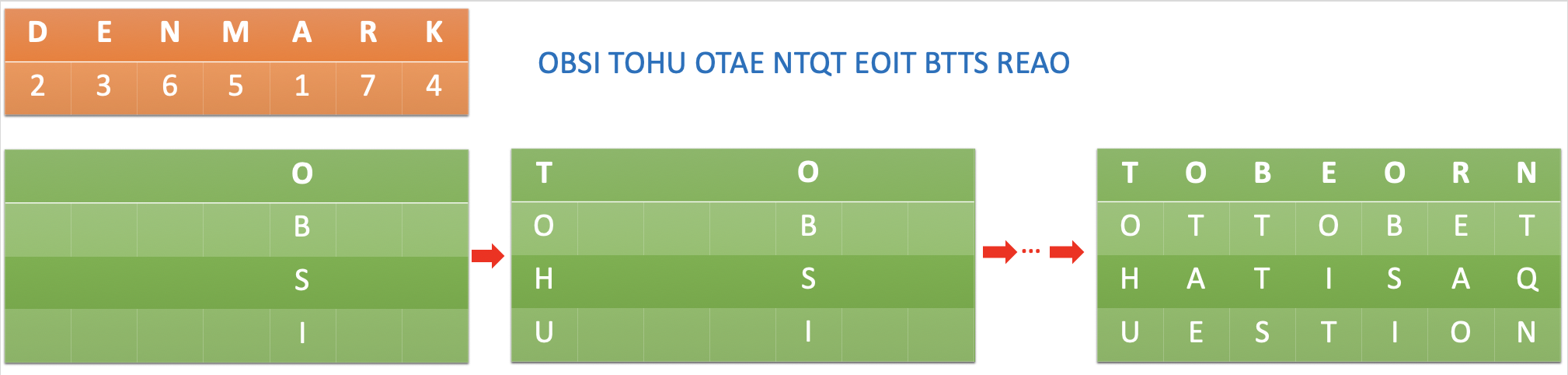
And we want to encrypt it using the key denmark.

Firstly we write the plaintext out in a grid. Note that the column number of the grid is the number of letters in the key. Since the key denmark has 7 letters, there are 7 columns:

Then we take the letters in the key in alphabetical order, and read down the columns in this order:

Therefore our ciphertext is OBSI TOHU OTAE NTQT EOIT BTTS REAO.

Note that if a letter is repeated, we do the one that appears first, then the next and so on. For example, if we changed our key to william, we should encrypt the plaintext like this:

The decryption process is pretty simple if we have the key. We have the key denmark, which has 7 letters, and we know the ciphertext is OBSI TOHU OTAE NTQT EOIT BTTS REAO, which has 28 letters. Therefore we can know there are 7 columns, and each column has 28/7 = 4 rows.

We can divide the ciphertext into 7 groups, each group has 4 letters. And according to the alphabetical order of the key, we can put each group as a column back to the grid:

Is this cipher secure? The answer is No. An attacker should firstly determine the length of the key, once the attacker has picked a key length, he/she can shuffle the columns around until they start to line up into meaningful fragments of text.

Given any ciphertext, attacker tries all possible values for the key. For a message of size n there are at most n possibilities for the key, hence attacker will obtain plaintext.

2. Substitution Cipher

The basic idea of substitution cipher is to substitute every plaintext character for a different ciphertext character. A simple version of substitution cipher is so-called Caesar cipher(the key of which is a single number).

A more complicated version is monoalphabetic substitution cipher, the keys of which usually consist of 26 letters. Here is an example key:

plain alphabet: abcdefghijklmnopqrstuvwxyz
cipher alphabet: phqgiumeaylnofdxjkrcvstzwb

Using the above key, we can encrypt our plaintext:

plaintext : To be or not to be that is a question
ciphertext: cd hi dk fdc cd hi cepc ar p jvircadf

The decryption process and the encryption process are invertible.

How many keys are there? When we choose a key, the letter a has 26 choices, and the letter b has 25 choices, c has 24 choices…so on and so forth. Therefore there are 26! ≈ 2^86 possible keys. Although there are many possiblities, we can use frequency analysis to break the cipher. Frequency of letter occurrence varies dramatically amongst letters. In English text, 12.7% of all letters are “e”, and 0.2% of all letters are “x”.

3. One-Time Pad

Again, we want to encrypt the sentence To be or not to be, that is a question, which has 28 letters. Suppose we have a 26-sided dice, we roll this dice for 28 times and obtain a pad of numbers:

9 4 9 24 26 5 9 2 9 2 7 26 26 26 25 12 9 17 21 25 25 4 24 21 16 5 4 14

Just like Caesar cipher, each of the above number is a “key”:

• The first number 9 is the key of the first letter t. As t is the 20th letter of the English alphabet, 20 + 9 = 3 mod 26, therefore the cipertext of t is c(the 3rd letter of the English alphabet).
• The second number 4 is the key of the second letter o. As o is the 15th letter of the English alphabet, 15 + 4 = 19 mod 26, therefore the cipertext of o is s(the 19th letter of the English alphabet).
• The thrid number 9 is the key of the third letter b…

As the process of generating key is totally random, the one-time pad is perfectly secure. The attacker cannot learn anything by looking at ciphertexts except the size of the ciphertext. But the one-pad time is not very practical, because the key is long (same length as the plaintext) and can be used only once.