Understanding Program Efficiency

Time complexity

Here is a piece of code:

sum(array):
    sum=0;
    n=array.length;
    for i=0;i<n;i++:
        sum+=array[i];
    return sum;

How do we measure the time efficiency of the above code? Assume these operations take constant time:

• mathematical operations
• comparisons
• assignments
• accessing objects in memory

Now we can count the operations in the above code:

Here is another piece of code:

search(array,target):
    n = array.length;
    for int i = 0; i<n;i++:
        if array[i] == target:
            return true;
    return false;

For this code, it is a little complicated to count the operations:

• In the best case, i.e., target is the first element in the array, it takes 5 operations to search the target.
• In the worst case, i.e., target is not in the array, it takes 3n+4 operations.
• In the average case, i.e., target is in the middle of the array, it takes 3n/2+4 operations.

From the above examples we can see that the count normally depends on the size of the inputs, therefore, we try to come up with a relationship between the size of the input and the count. We focus on what happens when the input is arbitrarily large, and only consider the worst case behavior(the upper bound).

In the first code, there are 4n+5 operations, which is linear. And if n is extremely large, the constant part 5 and the coefficient 4 become insignificant. Therefore, we use O(n) (big O notation) to represent the efficiency of this code, which is also called time complexity.

In the second code, by considering the worst case, there are 3n+4 operations. And by ignoring the insignificant part, we use O(n) to represent its time complexity.

Complexity Classes

Here is a comparison of different complexity classes:

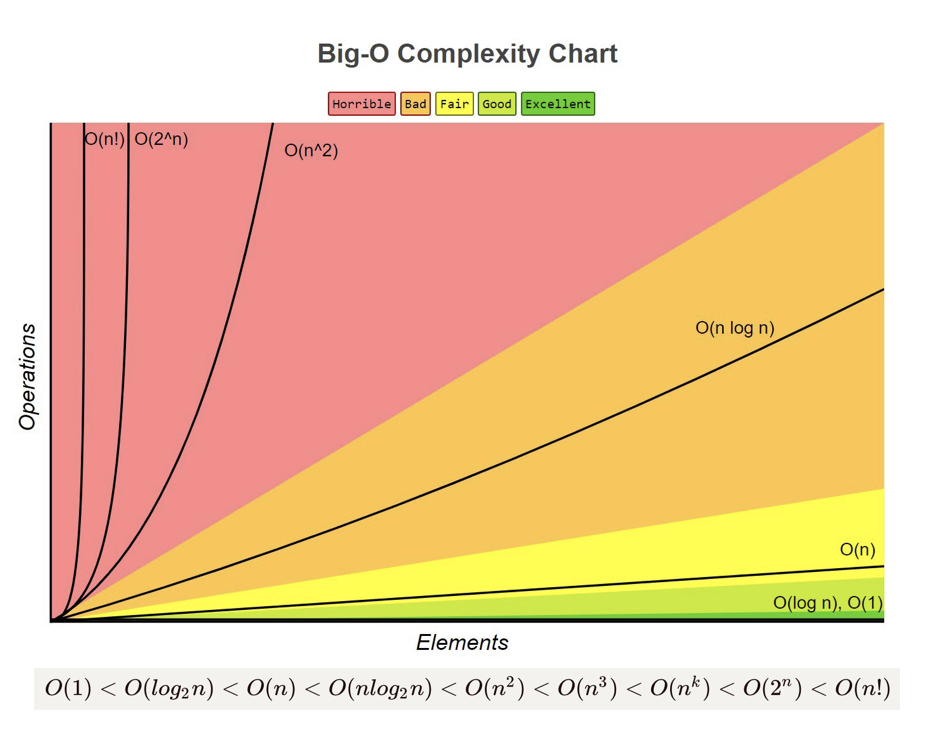
Now I am going to talk about some examples of these complexity classes.

Linear Complexity

From the examples in the beginning, we can see that simple iterative loop algorithms are typically linear in complexity. Some simple recursive algorithms are also linear, for example:

fact(n):
    if n <= 1:
        return 1
    else:
        return n*fact(n – 1)

The time complexity of above code can be computed in this way:

T(n) = T(n - 1) + O(1) 
     = T(n - 2) + O(1) + O(1) 
     = T(n - 3) + O(1) + O(1)+ O(1) 
     = ... 
     = O(1) + ... + O(1) +O(1) + O(1) 
     = n * O(1) 
     = O(n)

Polynomial Complexity

Nested loops are typically polynomial in complexity. Most common polynomial algorithms are quadratic, for example:

for i = 0; i < n; i++:
     for j = 0; j < 3n; j++:
         print i, j;

The inner loop goes 3n times and the outer loop goes n times. Therefore the time complexity of the above code is O(n)*O(3n) = O(n^2).

Some nested recursive algorithms are also polynomial.

Logarithmic Complexity

Binary search alogrithm is logarithmic in complexity. In binary search, we keep breaking a list into halves till there is only one element.

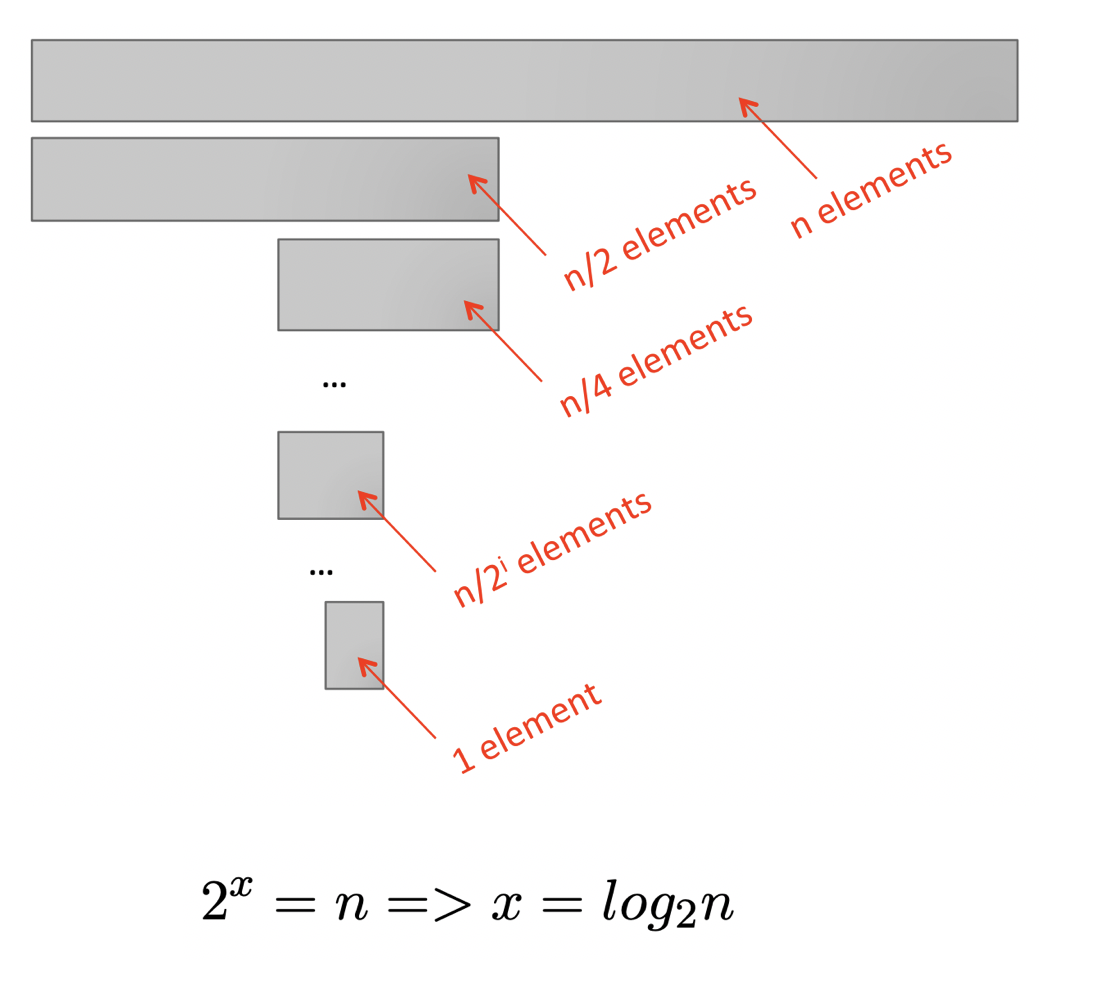
A while loop can also be logarithmic in complexity:

i = 1;
while (i < n):
   i = i * 2;

Log-linear Complexity

Merge sort alogrithm is log-linear in complexity. And here is a simple example which makes use of a for loop and a while loop:

for(int m = 1; m < n; m++){
   i = 1;
   while(i < n){
      i = i * 2;
   }
}

Exponential Complexity

Tower of Hanoi Problem is exponential in complexity.

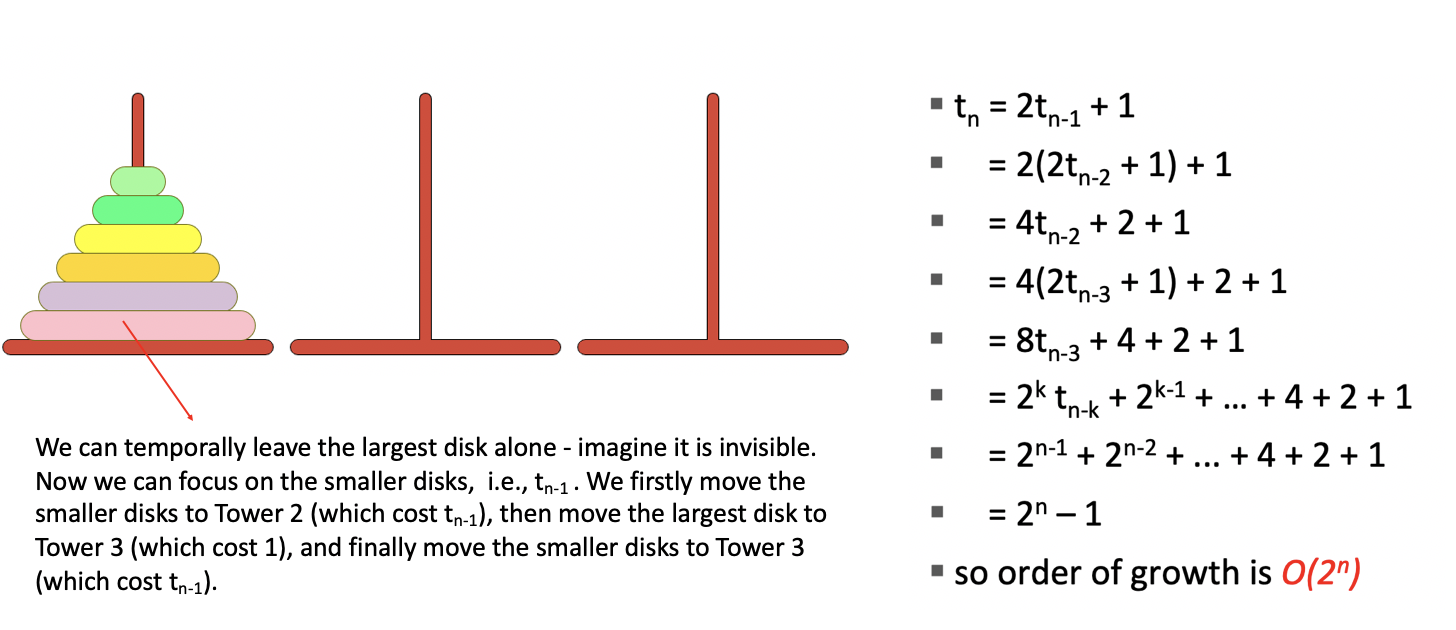
Algorithm Complexity VS Problem Complexity

What we talked above is Algorithm Complexity, which refers to the upper bound of a specific alogrithm, such as binary search and merge sort, etc.

There is another conception called Problem Complexity, which refers to the upper bound of the best solution of a specific problem. For example, the best solution of searching problem is binary search, therefore the problem complexity of searching is O(logn). And (one of) the best solution of sorting problem is merge sort, therefore the problem complexity of sorting is O(nlogn).

Now I want to briefly introduce P problems and NP problems. P problems is a class of problems that can be solved in polynomial time. While for NP problems, NP means Non-deterministic Polynomial. NP problems are hard to solve, but if we can “guess” a solution of a NP problem, we can check the solution in polynomial time. For example, a 100x100 Sudoku puzzle can take a long time to solve, but if I give you a solved Sudoku grid, we can check it quickly.