Reverse Polish Notation

algorithm

Reverse Polish Notation

Reverse Polish Notation(RPN) is used to represent expressions in which the operators are placed after the operands. For example, if we want to add two numbers a and b, we can write an expression like this:

`a+b`

This is called infix expression, because the operator + is between the operands a and b. And this expression can be represented in RPN as:

`a b +`

RPN can save the interpreter or the compiler a lot of effort in executing a expression. For example, here are two infix expressions:

`a+b×c`
`(a+b)×c`

We are all taught at school that multiplication takes precedence, therefore in the expression a+b×c, we firstly multiply b by c then add a. If we want the addition operation come first, we should use brackets, i.e., (a+b)×c. However, computers do not know that addition has a lower precedence, and it would be confusing for a computer to execute a+b×c directly. To address this problem, we can convert the expressions above in PRN:

`a+b×c=> abc×+`
`(a+b)×c=> ab+c×`

We can see that RPN can avoid the use of brackets and make it easier for computers to interpret and execute expressions. Therefore, when we want to execute a expression(infix) in computer, we can convert it into RPN first. A algorithm called shunting-yard can help us realise the conversion.

The shunting-yard algorithm makes use of two data structures stack and queue in the converting process:

1
2
3
4
5
6
7
8
9
10
11
12
Read an element in the infix expression
If it is a number(operand) add it to queue
If it is an operator:   
    While there is an operator on the top of the stack with greater or equal precedence:
        Pop operators from the stack onto the output queue
    Push the current operator onto the stack
If it is a left bracket, push it onto the stack
If it is a right bracket:
    While there is not a left bracket on the top of the stack:
        Pop operators from the stack onto the output queue
    Pop the left bracket from the stack and discard it
While there are operators on the stack, pop them to the queue

Here is an example of using the above algorithm. Consider an infix expression:

`15×(3 + 6)`

The first element is 15, which is a number, add it to queue:

rpn_1

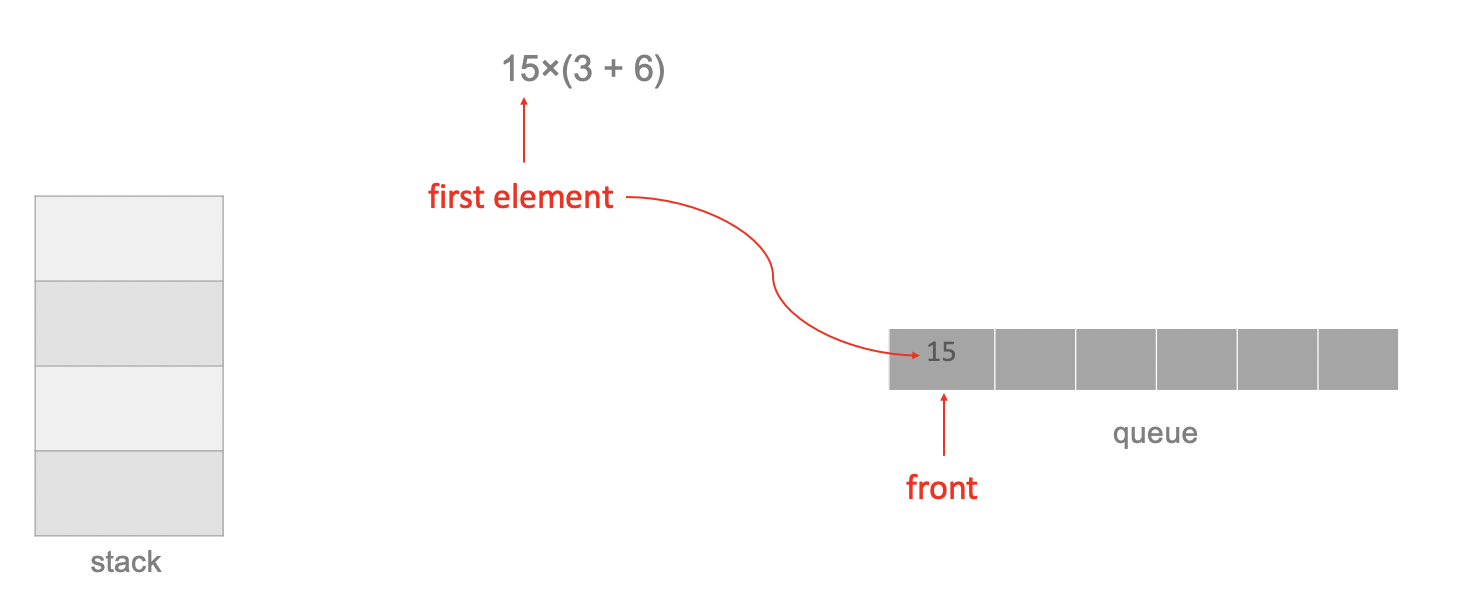
The second element is the operator ×, and there is no operator on the top of the stack, therefore push the operator × onto the stack:

rpn_2

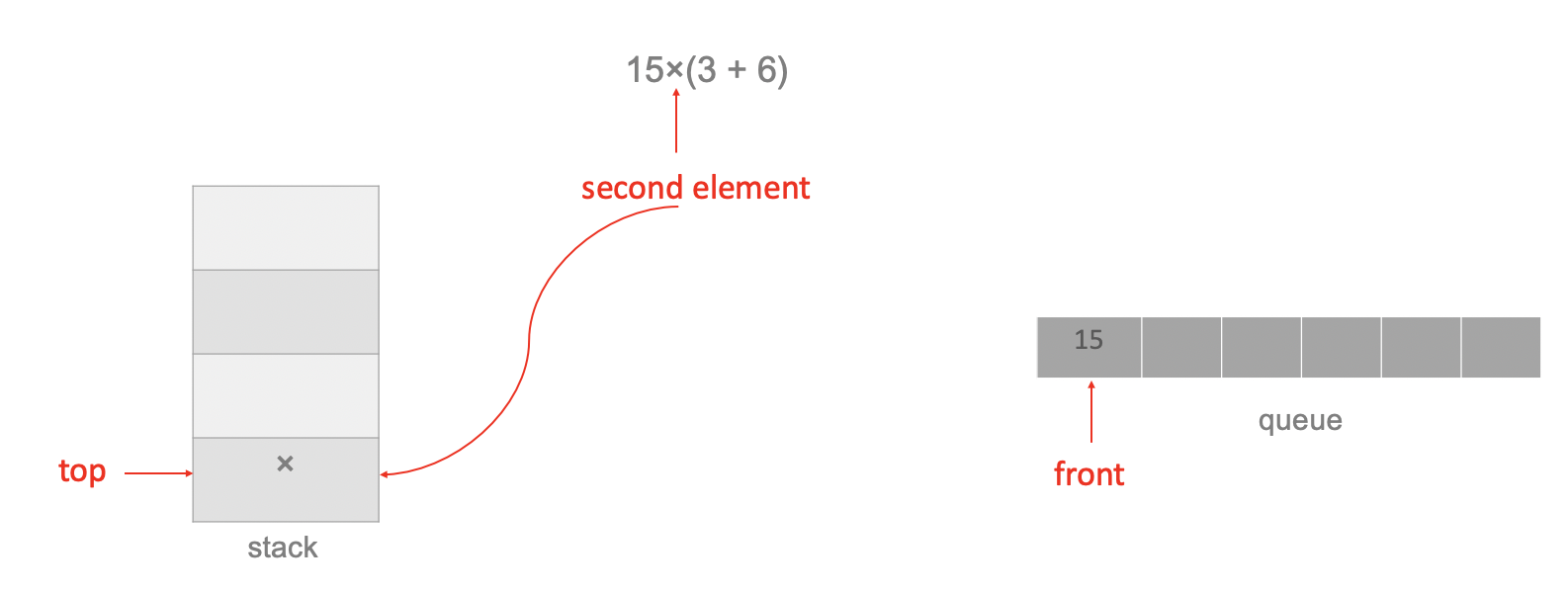
The third element is left bracket, push it onto the stack:

rpn_3

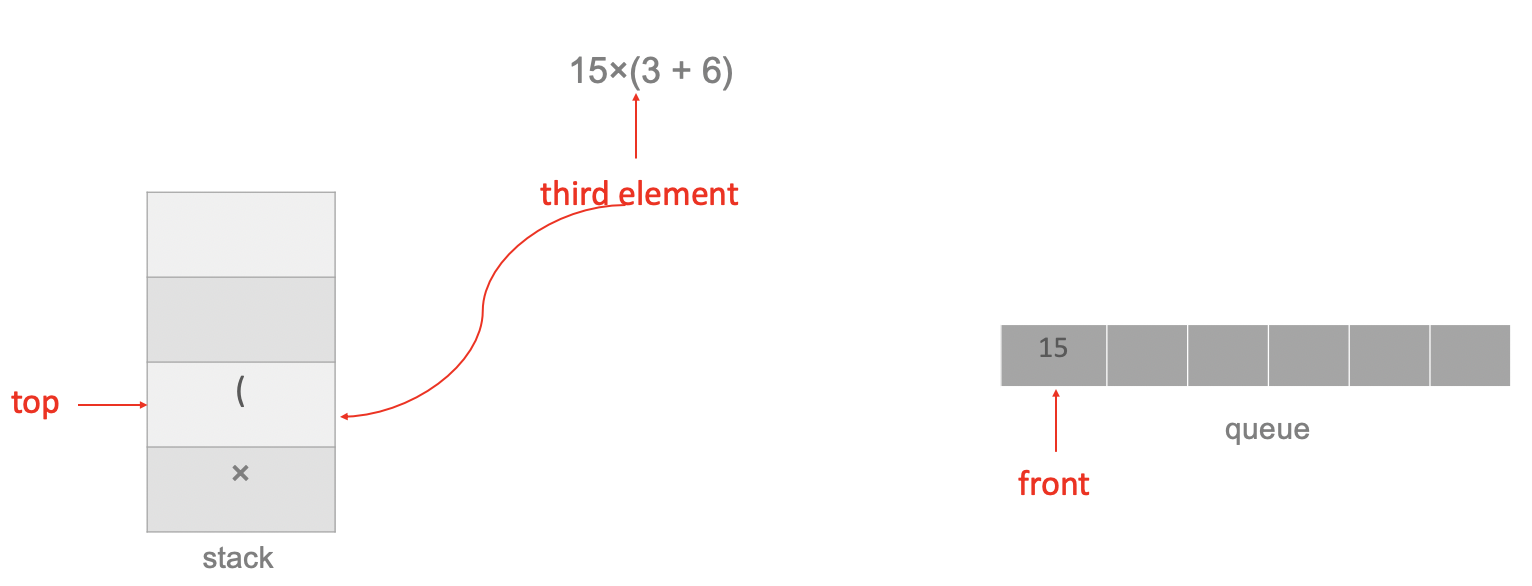
The fourth element is the number 3, add it to queue:

rpn_4

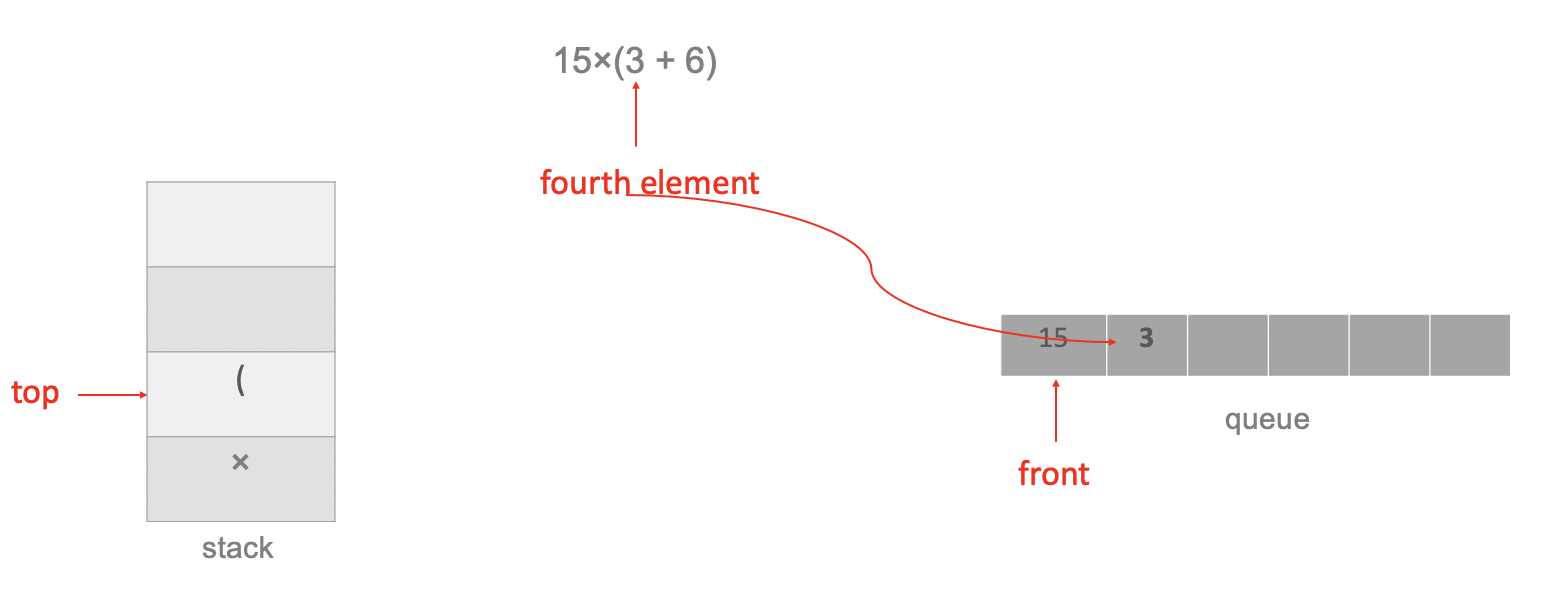
The fifth element is the operator +, and the top of the stack is not an operator, therefore push the operator + onto the stack:

rpn_5

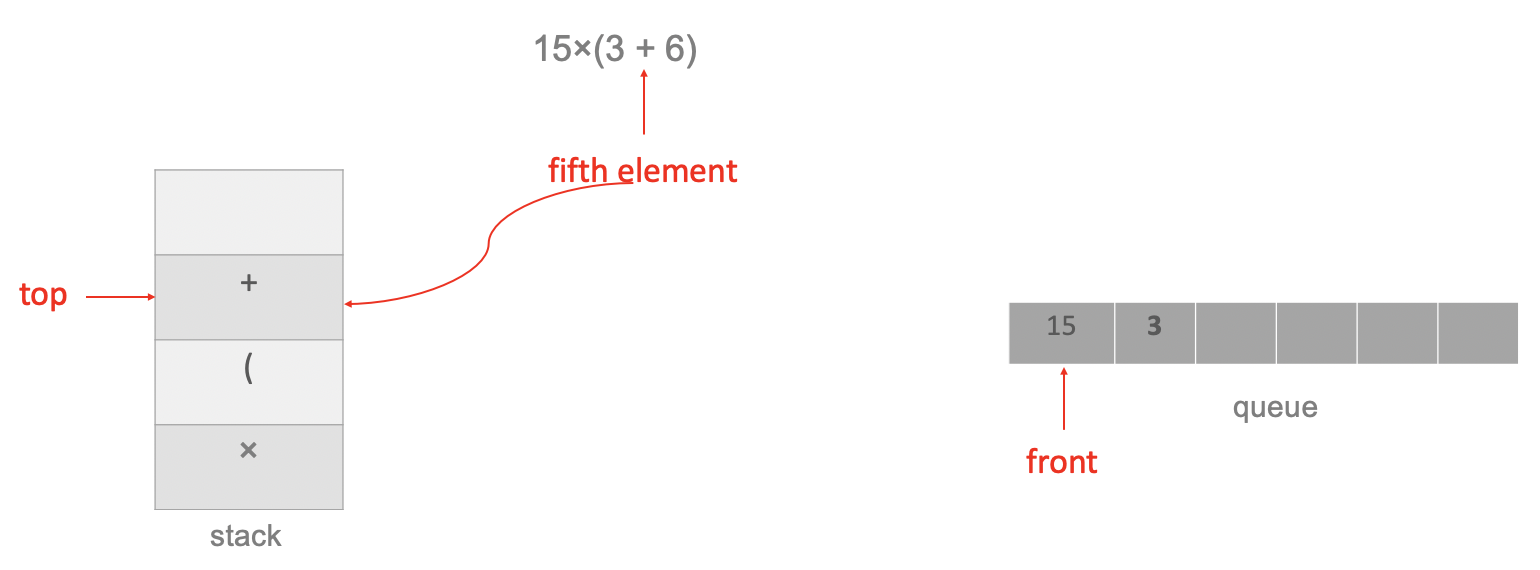
The sixth element is the number 6, add it to queue:

rpn_6

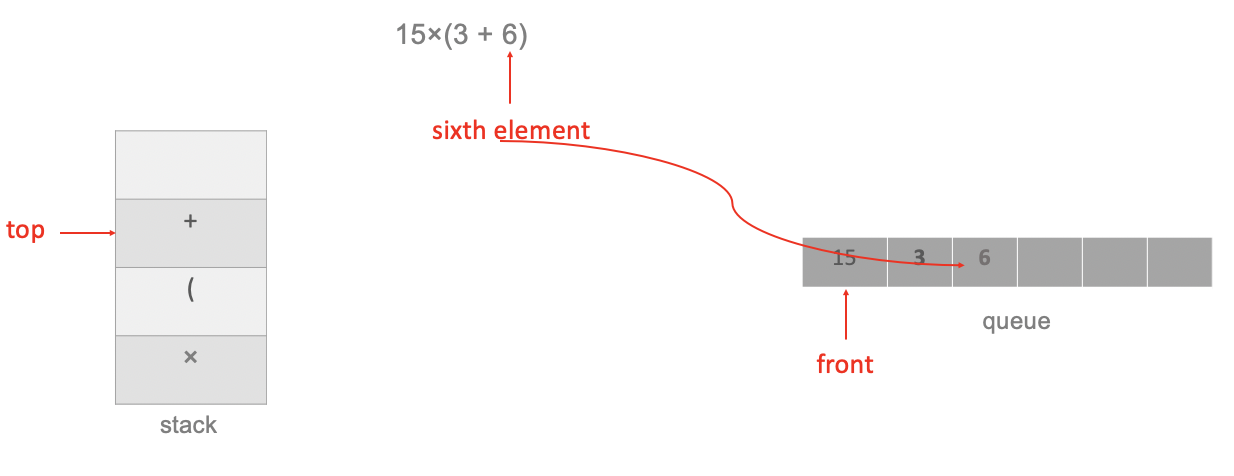
The last element is right bracket, and the top of the stack is not a left bracket, therefore, pop operators from the stack until there is a left bracket on the top of the stack:

rpn_7

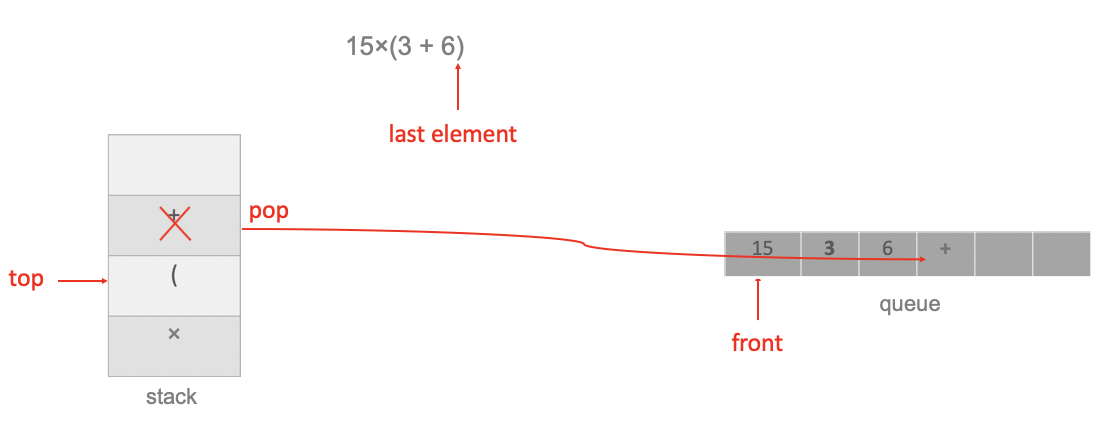
Pop the left bracket and discard it, then pop the operator × to the queue:

rpn_8

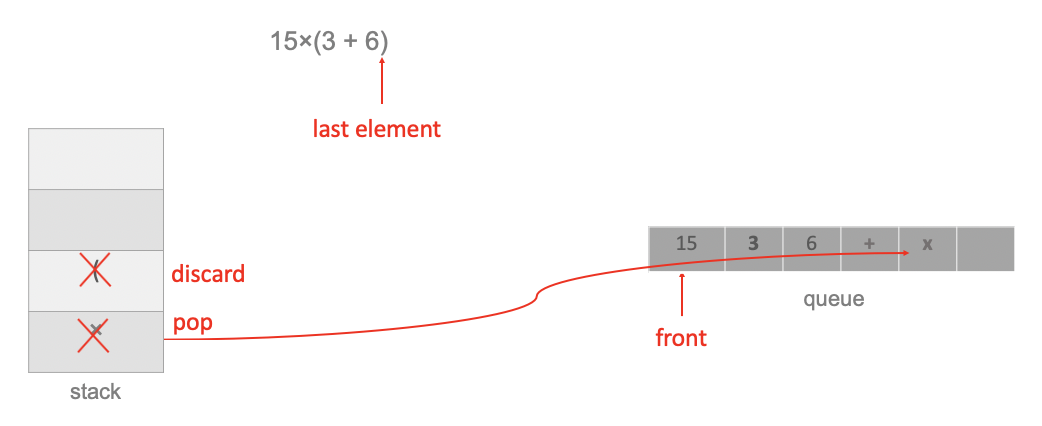
Now we read the elements in the queue from front to rear, which is the RPN of 15×(3 + 6):

`15 3 6 + ×`

Reading from left to right, this is interpreted as follows:

  1. Push 15 onto the stack
  2. Push 3 onto the stack. Reading from the top, the stack now contains (3, 15)
  3. Push 6 onto the stack. Reading from the top, the stack now contains (6, 3, 15)
  4. Apply the + operation: take the top two numbers off the stack, add them together, and put the result back on the stack. The stack now contains (9, 15).
  5. Apply the × operation: take the top two numbers off the stack, multiply them together, and put the result back on the stack. The stack now contains just the number 135, which is the final result of the expression.