How to represent negative numbers in computers

Computers sometimes need to work with negative numbers. This article introduces two methods for computers to represent negative numbers.

Using a sign bit

One method to represent negative numbers is to use a sign bit. Sign bit is the bit at the far left of the bit pattern, with 0 indicating a positive number and a 1 indicating a negative number. For example, 10001001 could represent -9, with the first bit(sign bit) indicating a negative number.

The smallest possible number using this method of representation is -127 (11111111) and the largest possible number is +127 (01111111). Besides, you might find that 00000000 represents 0 and 11111111 represents -0.

2’s complement

Most computers use 2’s complement representing negative numbers, which can be more effective when performing mathematical operations like adding and subtracting.

Here is an example of how to find -2 using 2’s complement numbers:

1. Find the corresponding positive binary value for the negative number. In this case, 2 = 0010.
2. Invert each bit of 2, namely 0010 => 1101.
3. Add 1 to this number: 1101 => 1110
4. And now, 1110 is -2 using two’s complement. In this way, the first bit 1 still works as a sign bit(1->negative, 0->positive). And we can using a simple way to convert this number to decimal number:

   -8 4 2 1 
   --------
    1 1 1 0
   
   1 * (-8) + 1 * 4 + 1 * 2 + 0 * 1 = -2

Another way to get -2 using 2’s complement is $2^n - (n-bit number)$, take 4-bit number as an example:

1. Find the corresponding positive binary value for the negative number. In this case, 2 = 0010
2. In this case we use 4-bit number, so $2^4 = 10000$
3. 10000 - 0010 = 1110, so -2 = 1110 using 2’s complement.
4. This method is quite simple, and we can spread it into other number systems. For example, in base 3, 121 in 3-bit 3’s complement is: $3^3 - (3-bit number) = 1000 - 121 = 102$

The smallest possible number using 2’s complement is -128 (or 10000000) and the largest possible number is +127 (01111111). And this time, there is only one 0(which is 00000000 in binary).

2’s complement addition

For example, -2 + 2 in 2’s complement binary can be calculated like this:

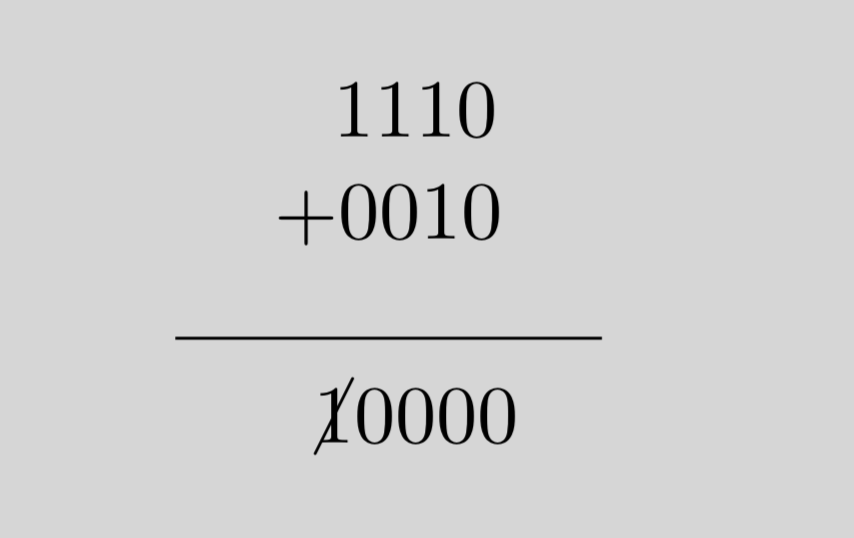
Note that in this example, the remaining carry number is simply discarded.

Overflow vs Carry

It is important to differentiate between an overflow and a carry. Let’s look at the comparison below:

As shown, in the overflow case, 1001 and 1010 are both negative numbers, while their sum is 0011, which is positive number. Therefore, it is overflow.

In the carry case, 1111 and 1100 are both negative numbers, and their sum is also negative. Therefore it is carry.

In conclusion, if the sum of two positive numbers is negative, or the sum of two negative numbers is positive, we can say it is an overflow. In other cases, it is a carry.