Computer Science: Number Systems

Base indicates how many digits are available within a numerical system. Decimal is known as base 10 because there are ten choices of digits between 0 and 9. For binary numbers there are only two possible digits available: 0 or 1. Therefore the binary system is also known as base 2.

This article will introduce how to convert numbers from base[2,8,10,16] ⟷ base[2,8,10,16].

1. Base 2 -> Base 10

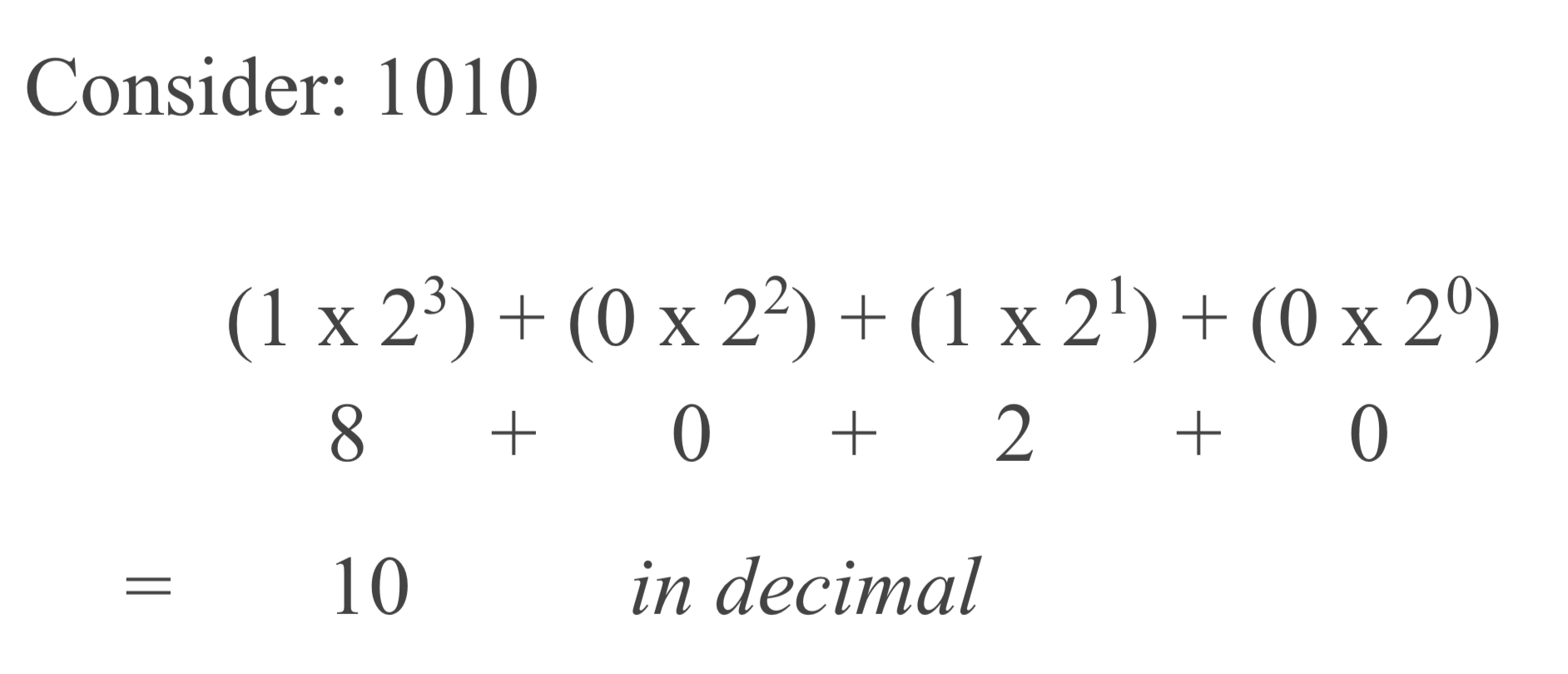
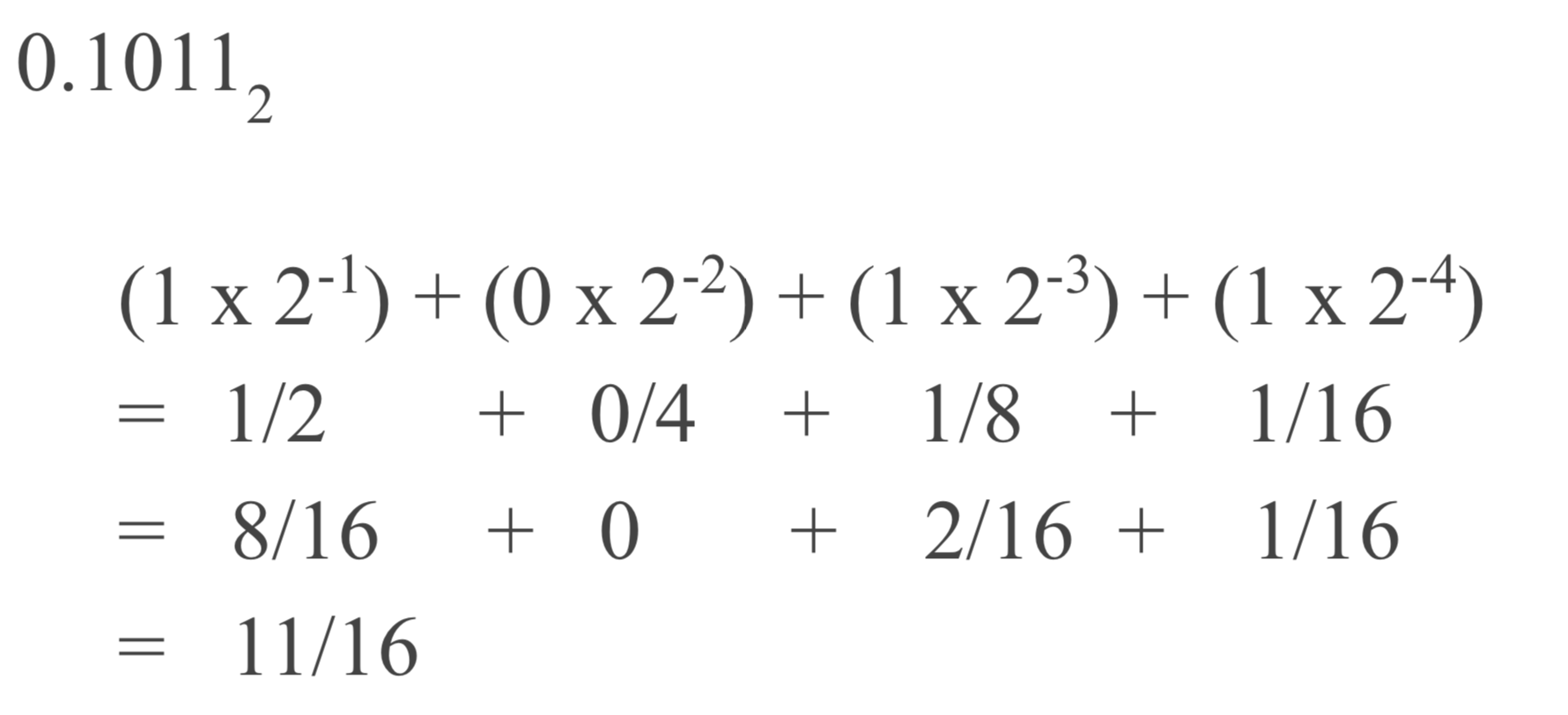
base 8 -> base 10 and base 16 -> base 10 is same as base 2 -> base 10 (just replace 2 with 8 or 16).

Why we use Base 2? Base 2 has two digits which can easily be represented on a computer by two states ON and OFF. Therefore,using Base 2 (or Binary) is easy for computers.

Why we use Base 8 and Base 16? Base 8 and Base 16 are used to compress binary digits. Each octal digit represents three binary digits, and each hexadecimal digit represents four binary digits. For example, we know that #FF0000 is hex color red. If we use Base 2 to represent red color, there would be a long string of numbers. We can also use Base 10 to compress binary digits, but compared to Base 8 and Base 16, it is more complicated converting binary numbers to decimal numbers.

2. Base 10 -> Base 2

For integers, the algorithm is simple: Divide the decimal number by 2 keeping notice of the quotient and the remainder. Continue dividing the quotient by 2 until you get a quotient of zero. Then just write out the remainders in the reverse order.

base 10 -> base 8 and base 10 to base 16 is same as base 10 -> base 16 (divide by 8 or 16 instead of 2).

Why does the algorithm mentioned above work? Here’s a simple explanation: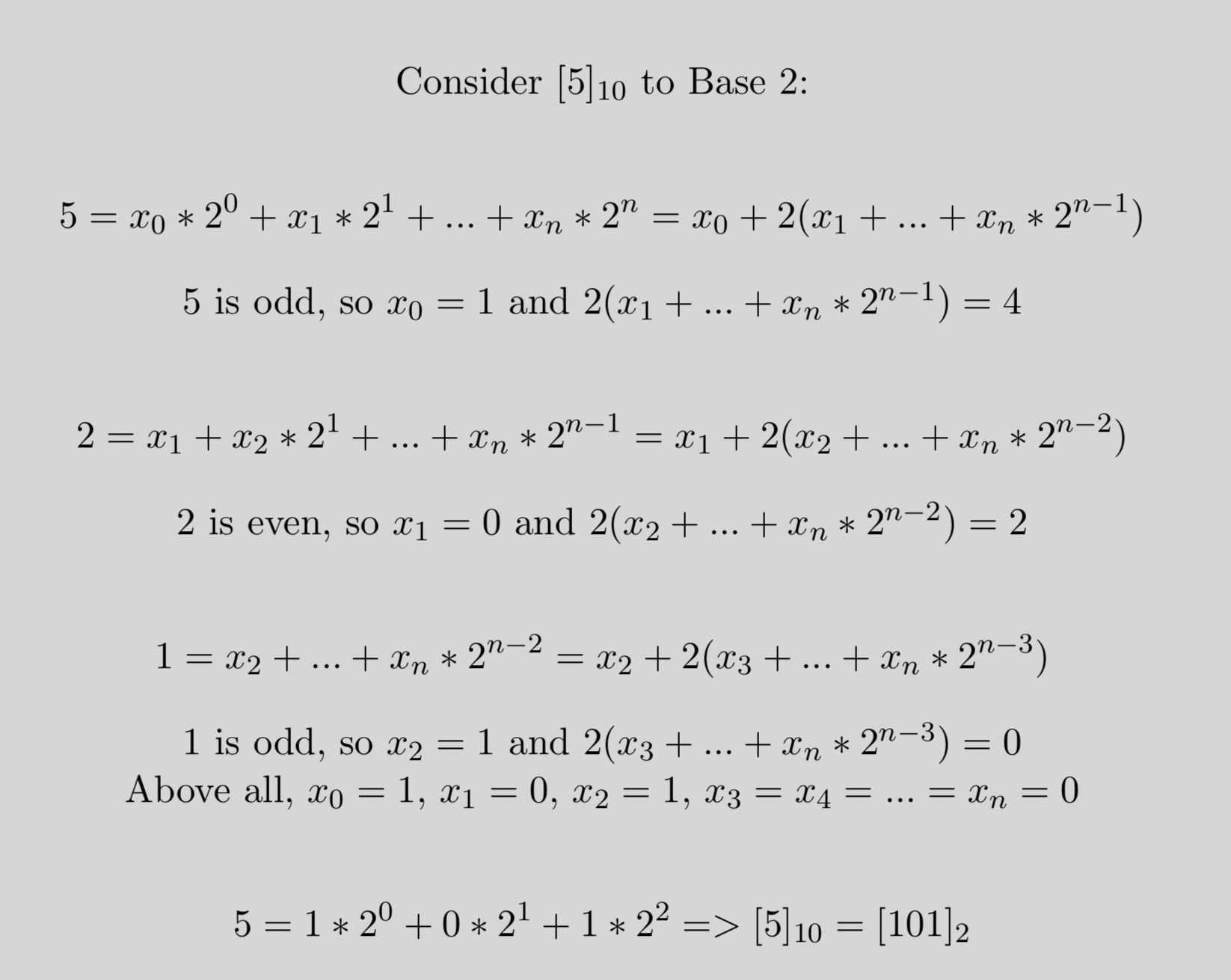

As for floating numbers, the algorithm is opposite, i.e., continue multiplying 2 until the fractional part of the floating number is 0, then just write out the integral part in order:

3. Base 2 -> Base 8

The largest number we can count using 3 digits in Binary is 7(i.e. 111 in binary). And the largest number we can count using 1 digit in Base 8 is 7. Therefore, each octal digit can replace 3 binary digits:

Similarly, in the case of Base 2 -> Base 16, each hexadecimal digit can replace 4 binary digits.

4. Base 8 -> Base 2

5. Binary Arithmetric

In the case of binary substraction, when I borrow 1, I always get 10(which means 2).